B.2 Angular Resolution Test
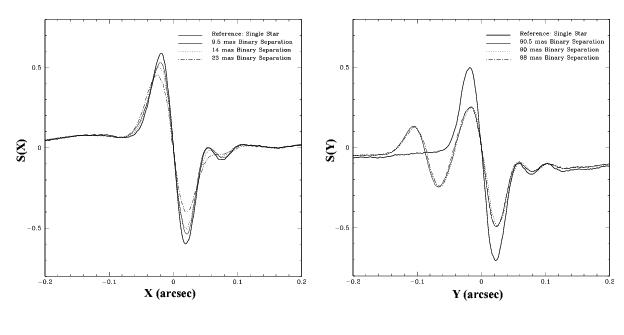
Following the FGS1r re-optimization in early May 1998, STScI executed a test to determine the angular resolution limits of FGS1r and FGS3 by observing a known binary system at several small increments of telescope roll angle. The binary ADS11300 is an 9th magnitude system with components having a magnitude difference Δm = 0.6. At the time of the test, the predicted angular separation of the components was 0.085" (Franz and Wasserman, private communication). The test was designed such that the predicted position angle of the binary was (almost) aligned with the Y axis of the FGS, i.e., the projected angular separation of the two stars was large along the Y axis but small along the X axis. By rolling the HST in 6 increments, the projected separation along the X axis varied from the predicted angular resolution limit of FGS1r (~6 mas) to the resolution limit of FGS3 (~20 mas).
The true position angle and separation of the components were determined from both the FGS1r and FGS3 observations with the stars separated by 23 mas along the X axis. These values were used to determine the actual angular separation of the stars along FGS1r’s X axis as a function of spacecraft roll, and the Transfer mode observations were analyzed to assess the instrument’s ability to measure these separations. The test included actual separations of 7, 9, 12, 14, 17, and 23 mas (as compared with the intended separations of 6, 8, 10, 12, 15, and 20 mas).
FGS3 was tested only at the component separations of 14 and 23 mas since simulations of its X axis performance indicated that this instrument would not “resolve” the binary for separations less than 20 mas.1
B.2.1 Test Results: The Data
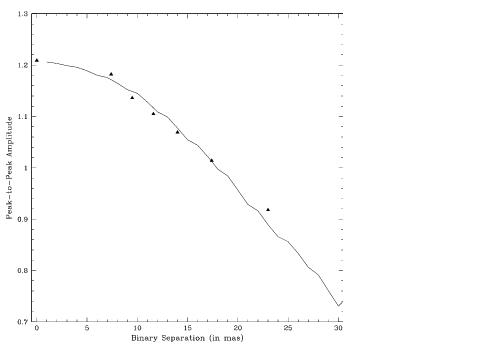
For the six observations with FGS1r, Figure B.5 compares the observed Transfer functions, and hence the response of the instrument to the angular separation of the stars as projected along the interferometer’s X- and Y-axis. It is evident from these data that FGS1r easily detected the non-singularity of the source, and is sensitive to the change in separation of the two stars. Figure B.6 plots the predicted vs. observed amplitude of the Transfer Function as a function of the binary’s projected separation.
Table B.1: FGS1r Angular Resolution Test: Effective Signal-to-Noise Ratios
Angular Separation | Peak-to-Peak Amplitude | S/N |
|---|---|---|
Single star | 1.209 | – |
+7.4 | 1.182 | 48.9 |
+9.5 | 1.136 | 63.2 |
+11.7 | 1.105 | 105.7 |
+14.0 | 1.069 | 128.6 |
+17.4 | 1.014 | 156.7 |
+23.0 | 0.918 | 194.7 |
B.2.2 Test Results: Binary Star Analysis
The observations were analyzed, as described in Appendix B: FGS1r Performance Summary, by finding a linear superposition of point source S-Curves that have been scaled and shifted to reproduce the observed Transfer function. Two separate techniques were employed. The most general model solves for the magnitude difference, angular separation, and parity of the binary’s components. The second technique constrains the magnitude difference and solves for both the separation and parity.
Table B.1 reports the results of these fits along the X axis for the FGS1r observations. In this table, a negative separation corresponds to a parity such that the faint star is to the “left” of the bright star, i.e., it is displaced in the –X direction of the scan. Likewise, a positive separation places the faint star to the right of the bright star. For these observations, the parity was positive so a negative parity is incorrect. The formal error of each of these fits is about 0.5 mas.
Along the Y axis, where the components are widely separated by about 90 mas, the fits to the Transfer functions yielded accurate results for both the FGS1r and FGS3 observations.
The FGS3 observations succeeded in detecting the non-singularity of the source when the stars were separated by 14 mas along its X axis, but could not yield an accurate measurement of the separation. The observation with the 23 mas separation succeeded (as expected).
Table B.2: FGS1r Angular Resolution Test: Binary Star Analysis
| Predicted Angular Separations (in mas) | Computed Separations (in mas) | |
|---|---|---|
| No Constraints Δmag Constrained | ||
+7.4 | +6.9 | +7.5 |
+9.5 | –11.1 | +11.5 |
+11.7 | –12.2 | +12.5 |
+14.0 | +13.6 | +14.1 |
+17.4 | +16.9 | +18.0 |
+23.0 | +23.0 | +23.0 |
For FGS1r, as can be seen in Table B.2, the unconstrained solution yields an incorrect parity for angular separations less than 14 mas. The models that constraining the magnitude difference reproduced the correct angular separations to within ~5%, even at the smallest separation of 7.3 mas (though, not for the test at 9.5 mas separation).
1 We express our greatest appreciation to O. Franz and L. Wasserman for researching the binary.