3.2.3 Solar System Targets Position Levels 2 and 3
The Solar System Targets form is used to specify moving targets in some HST observations. This article provides a description of the Level 2 and 3 specifications needed for the Astronomer’s Proposal Tool (APT). |
|---|
On This Page
Target Position Level 2 [Level_2]
Six Target Reference Systems (TRSs) are described in the following paragraphs. Please pay careful attention to the definitions of each TRS. Specify your target in one of the following ways:
STD = <object name> or TYPE = <name>
In this case <object name> is from the list of 3.2.1 Solar System Standard Targets, or the Type is:
PGRAPHIC
planetographic coordinates relative to Level 1 target
POS_ANGLE
polar coordinate offsets from Level 1 target
MAGNETO
position in magnetic coordinate system
TORUS
line-of-sight projected coordinate system
SAT
orbital elements of a satellite
PCENTRIC
planetocentric coordinates relative to Level 1 target
For the PGRAPHIC, MAGNETO, and TORUS coordinate systems, the north pole is defined to be the rotational pole in the northern celestial hemisphere. For planets with direct rotation, the angular momentum vector coincides with the north pole. For planets with retrograde rotation, the angular momentum vector coincides with the south pole.
Planetographic Coordinate System
Table 3.18: Parameters for TYPE = PGRAPHIC
| LONG = <value> | planetographic longitude in degrees |
| LAT = <value> | planetographic latitude in degrees; use – to denote south latitude |
| [ALT = <value>] | planetographic altitude above the reference ellipsoid, in kilometers |
[R_LONG = <value>]1 | rate of change of planetographic longitude, in degrees/day |
| [R_LAT = <value>]1 | rate of change of planetographic latitude, in degrees/day |
| [R_RAD = <value>]1 | rate of change of planetographic altitude, in kilometers/day |
| [EPOCH = <value>] | the reference time for the temporal variation, in TDB, TDT or UTC2 |
1 EPOCH must also be specified with this quantity.
2 TDB (Barycentric Dynamical Time), TDT (Terrestrial Dynamic Time), UTC (Coordinated Universal Time)
The PGRAPHIC TRS is the IAU planetographic coordinate system. It is a non-spherical coordinate system aligned with and rotating about the rotation axis of the Level 1 body, positive north, whose origin lies at the center of the reference body. Locations within this TRS are specified by longitude, latitude, and altitude above the surface, and are tracked as the object rotates. (The lambda(III) coordinate system defines the prime meridian in this coordinate system; if lambda(I) or lambda(II) coordinate systems are desired, note this in the Comments field.)
Planetographic Latitude is defined as the angle between the equator and the normal to the surface of the reference ellipsoid at the point of interest.
By definition, the planetographic longitude of the sub-Earth point increases with time. For planets with direct rotation, the planetographic longitude increases in a left-handed direction (to the West). For planets with retrograde rotation, the planetographic longitude increases in a right-handed direction (to the East). Longitudes should be specified in degrees West for planets with direct rotation and degrees East for planets with retrograde rotation.
If ALT is omitted, then the surface of the reference ellipsoid is assumed.
If the coordinates are constant in time, then none of the other optional entries should be used. If any coordinate is given as a function of time, then EPOCH is required and the time-varying coordinate is interpreted in the following way.
Example:
LONG = 20
LAT = -5
R_LONG = 45
EPOCH = 5-JAN-1990:15
For this example the longitude at any time, T, is given by: longitude = LONG + R_LONG * (T – EPOCH)
or, numerically,
longitude = 20 + 45 * (t – 5–JAN–1990:00:15:00)
Position Angle Coordinate System
Table 3.19: Parameters for TYPE = POS_ANGLE
| RAD = <value> | Radius, in arcseconds |
| ANG = <value> | Position angle relative to the reference axis, in degrees |
REF = NORTH REF = SUN | Reference axis is celestial north, or Reference axis is the apparent direction to the Sun as projected on the sky |
| [R_RAD = <value>]1 | Rate of change of radius, in arcseconds/day |
| [R_ANG = <value>]1 | Rate of change of position angle, in degrees/day |
| [EPOCH = <value>] | the reference time for the temporal variation, in TDB, TDT or UTC2 |
1 EPOCH must also be specified with this quantity.
2 TDB (Barycentric Dynamical Time), TDT (Terrestrial Dynamic Time), UTC (Coordinated Universal Time)
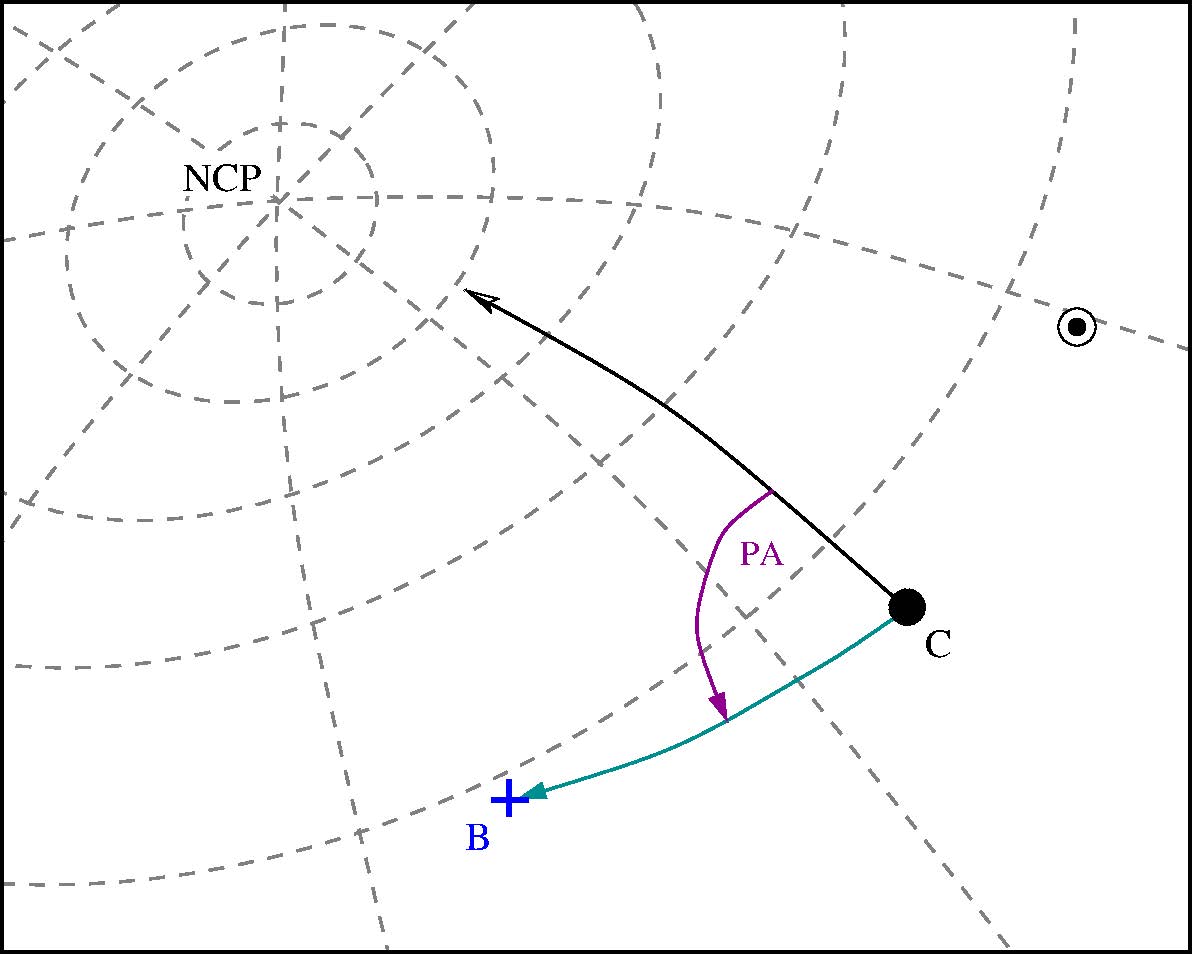
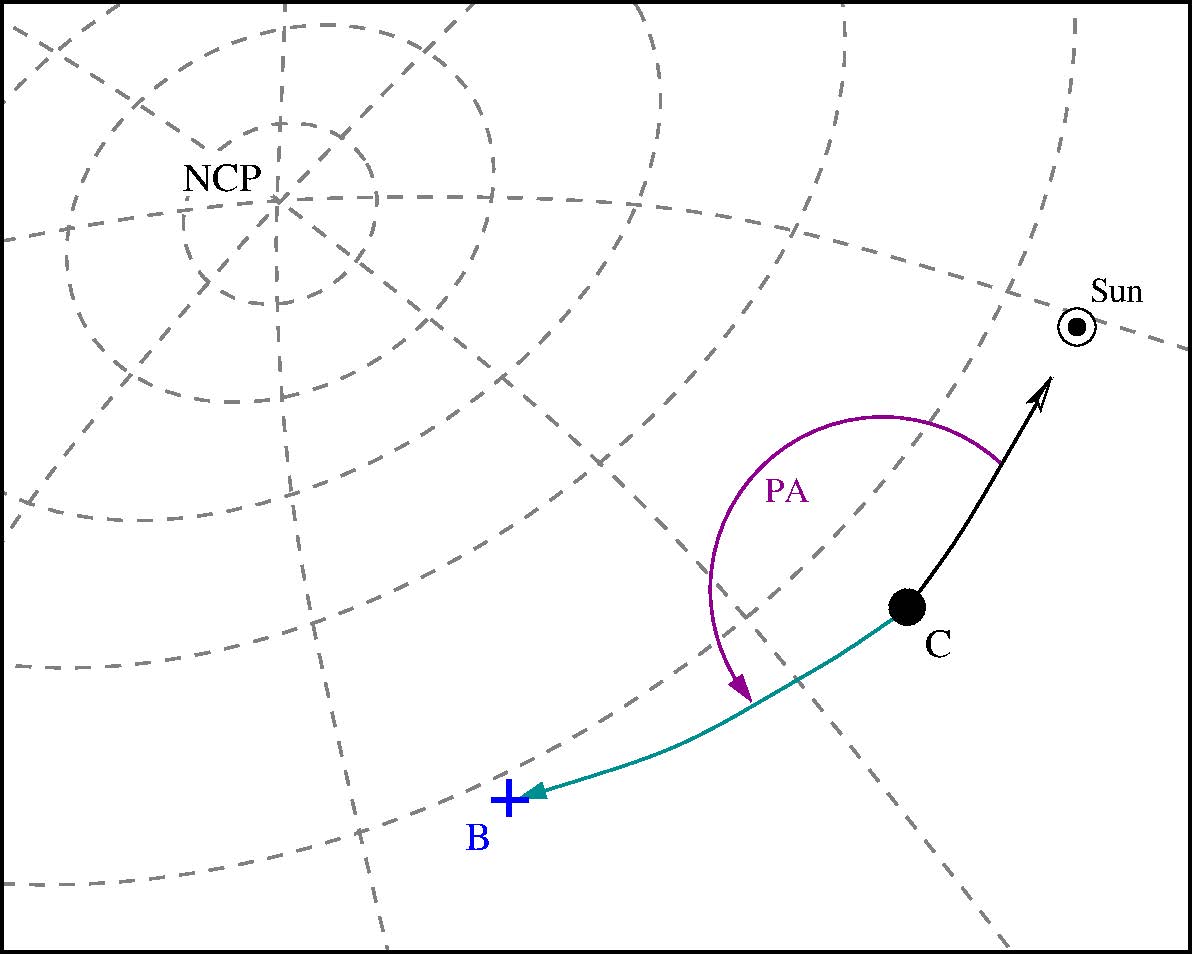
The POS_ANGLE TRS is a position-angle coordinate system (i.e. a two-dimensional polar-coordinate system). This TRS is useful for pointing at targets whose positions are known only in terms of an offset in projected celestial coordinates from another body. The origin of the system lies at the center of the Level 1 body. Locations are specified by giving the apparent distance from the origin (in projected celestial coordinates as viewed from the Earth) and the position angle from some reference axis to the target point.
When REF = NORTH the reference meridian passes through celestial north; and ANGLE is measured counter-clockwise from north through east. The RADIUS is the angular separation of the Level 2/3 object from the center of Level 1/2 object along this position angle, as shown in the following diagram.
When REF=SUN the reference meridian passes through the apparent Sun (as seen from the observer), and ANGLE is measured counter-clockwise as seen on the sky. The RADIUS is the angular separation of the Level 2/3 object from the center of Level 1/2 object along this position angle, as shown in the following diagram.
Magnetic Coordinate System
Table 3.20: Parameters for TYPE = MAGNETO
| LONG = <value> | Magnetic longitude, in degrees |
| LAT = <value> | Magnetic latitude, in degrees; use – to denote south latitude |
| RAD = <value> | Magnetic radius, in kilometers |
| [POLE_LAT = <value>] | Cartographic latitude of the pole, in degrees |
| [POLE_LONG = <value>] | Cartographic longitude of the pole, in degrees |
| [O_LAT = <value>] | Cartographic latitude of the origin in degrees; use – to denote south latitude |
| [O_LONG = <value>] | Cartographic longitude of the origin in degrees |
| [O_RAD = <value>] | Cartographic radius of the origin, in kilometers |
The MAGNETO TRS is intended to support observations fixed with respect to a planetary magnetic field. It is a spherical coordinate system rotating with the Level 1 body around the rotation axis, with a specified offset of the coordinate origin and inclination of the coordinate pole. The MAGNETO coordinate system is defined in the following manner:
- Define a “cartographic” reference frame identical to the planetographic TRS, except use spherical latitudes.
- Rotate the new coordinate system relative to the cartographic frame so the new pole is located at POLE_LAT (latitude) and POLE_LONG (longitude).
- The final step is to translate the origin of the new system to the specified cartographic latitude, longitude, and radius (O_LAT, O_LONG, and O_RAD, respectively).
While the origin and coordinate axes may differ from those of the cartographic system, the rotation axis and rotation rate are identical to those of the cartographic system. Locations in the MAGNETO TRS are specified by longitude, latitude, and radius from the origin of the defined coordinate system, and are tracked as the object rotates.
Torus Coordinate System
Table 3.21: Parameters for TYPE = TORUS
| LONG = <value> | Torus longitude, in degrees |
| LAT = <value> | Torus latitude, in degrees; use – to denote south latitude |
| RAD = <value> | Torus radius, in kilometers |
| [POLE_LAT = <value>] | Cartographic latitude of the pole, in degrees |
| [POLE_LONG = <value>] | Cartographic longitude of the pole, in degrees |
| [O_LAT = <value>] | Cartographic latitude of the origin in degrees; use – to denote south latitude |
| [O_LONG = <value>] | Cartographic longitude of the origin in degrees |
| [O_RAD = <value>] | Cartographic radius of the origin, in kilometers |
If the optional fields above are left blank, they default to the nominal values for the Jupiter magnetic coordinate frame:
O_LONG = 0
O_LAT = +0
O_RAD = 0
POLE_LAT = +83
POLE_LONG = 202
The TORUS TRS is defined primarily to support observations of Jupiter's plasma torus and is closely related to the MAGNETO TRS. The difference between the two systems is in the definition of the prime meridian. For the TORUS TRS, the prime meridian is defined by the instantaneous longitude of the sub-observer point.
TORUS can also be useful for observers who want to observe in a coordinate system that is fixed relative to the apparent disk of the Level 1 body, e.g. central meridian observations. If the TORUS center is defined to be the same as the center of its associated Level 1 body:
O_LONG = 0
O_LAT = +0
O_RAD = 0
POLE_LAT = +90
then, in that case, the TORUS TRS will not rotate with the Level 1 body. If the TORUS center is defined differently from the Level 1 body center, then the polar axis of the TORUS TRS will precess with the Level 1 body's rotation.
A typical observation would be of the east or west ansa (point of maximum elongation) of an equatorial circle whose radius is roughly five times the equatorial radius of Jupiter (in this case, LONG = 270 (90 for the west ansa), LAT = 0, RAD = 3.57E05). This coordinate system can also be used to support observations of a planetary ring ansa.
Satellite Elements Coordinate System
Table 3.22: Parameters for TYPE = SAT
| A = <value> | Semi-major axis of satellite orbit, in km |
| EPOCH = <value> | Epoch of the elements, in TDB, TDT or UTC1 |
| N = <value> | Mean motion of satellite, in degrees/day |
| L = <value> | Mean longitude at EPOCH, in degrees |
| [E = <value>] | Eccentricity of satellite orbit |
| [I = <value>] | Inclination of satellite orbit to the planetary equator, in degrees |
| [O = <value>] | Longitude of ascending node of the satellite orbit, in degrees |
| [W = <value>] | Longitude of periapse, in degrees |
| [O_RATE = <value>] | Rate of change of longitude of ascending node, in degrees/day |
| [W_RATE = <value>] | Rate of change of periapse, in degrees/day |
| [RAP = <value>] | Right Ascension of the parent planet pole at EPOCH |
| [DECP = <value>] | Declination of the parent planet pole at EPOCH |
| [EQUINOX = <value>] | B1950 or J2000 |
1 TDB (Barycentric Dynamical Time), TDT (Terrestrial Dynamic Time), UTC (Coordinated Universal Time)
When the target is a satellite of the object defined in the Level 1 field, but the satellite itself is not among the standard targets, then orbital elements must be specified. These elements refer to the motion of the satellite around the Level 1 object.
The “reference” axis for the angles defined above is the intersection of the Earth’s equator at the standard epoch implied by the EQUINOX with the parent planet’s equator at the EPOCH of the elements. The positive X-axis for the coordinate system used in the orbit calculation is obtained by taking the cross product of the Z-axis of the standard system (i.e. the system defined by the standard equator and equinox given by EQUINOX) with the pole of the planet. If E, I, O, W, O_RATE, and W_RATE are not supplied, then their values are assumed to be 0. If RAP and DECP are not supplied, then the standard IAU values are used. If RAP and DECP are supplied, then they should be referred to the standard equator and equinox given by EQUINOX. If EQUINOX is not provided, we will assume J2000.
STScI maintains its ephemeris database with the best available elements, and you should use the STD = form for objects in the list of 3.2.1 Solar System Standard Targets unless there is compelling scientific justification for specifying orbital elements.
Planetocentric Coordinates
PCENTRIC: planetocentric coordinates relative to Level 1 target
For the PCENTRIC coordinate system, the north pole is defined to be the rotational pole in the northern celestial hemisphere. For planets with direct rotation, the angular momentum vector coincides with the north pole. For planets with retrograde rotation, the angular momentum vector coincides with the south pole.
Table 3.23: Parameters for TYPE = PCENTRIC
| LONG = <value> | planetocentric longitude, in degrees |
| LAT = <value> | planetocentric latitude, in degrees; use – to denote south latitude |
| RAD = <value> | planetocentric radius, in kilometers |
| [R_LONG = <value>]1 | rate of change of planetocentric longitude, in degrees/day |
| [R_LAT = <value>]1 | rate of change of planetocentric latitude, in degrees/day |
| [R_RAD = <value>]1 | rate of change of planetocentric radius, in kilometers/day |
| [EPOCH = <value>] | the reference time for the temporal variation, in TDB, TDT or UTC2 |
1 EPOCH must also be specified with this quantity.
2 TDB (Barycentric Dynamical Time), TDT (Terrestrial Dynamic Time), UTC (Coordinated Universal Time)
The PCENTRIC TRS is the IAU planetocentric coordinate system. It is a right-handed spherical coordinate system aligned with and rotating about the rotation axis of the Level 1 body, positive north, whose origin lies at the center of the Level 1 body. Locations within this TRS are specified by longitude, latitude, and radius from the origin, and are tracked as the object rotates. (The lambda(III) coordinate system defines the prime meridian in this coordinate system; if lambda(I) or lambda(II) coordinate systems are desired, note this in the Comments field.)
Planetocentric longitude is always measured positively to the east relative to the prime meridian, regardless of which way the planet rotates. East is defined as the counter-clockwise direction around the planet, as seen from above its north pole, and the north pole is whichever pole more closely aligns with the Earth's north pole. Imagine a distant, non-orbiting observer viewing a directly rotating planet. Also, suppose that this observer is within the plane of the planet's equator. A point on the Equator that passes directly in front of this observer later in time has a lower planetocentric longitude than a point that did so earlier in time.
If RAD is omitted, then RAD is assumed to be the equatorial radius of the Level 1 body. Note that in general, if RAD is omitted, the point specified will not necessarily be on the visible surface of the planet. This is of special concern for oblate planets, e.g. Jupiter and Saturn, where a point at high latitude at the equatorial radius can appear above the limb of the planet in projection. When using this coordinate system for surface features on Jovian planets, it is best to specify the radius explicitly.
For spherical planets, planetographic and planetocentric latitudes are identical. For significantly nonspherical objects, there is no simple conversion between the two latitude systems.
For planets with retrograde rotation, the planetocentric and planetographic longitudes of a point are identical. For planets with direct rotation, the planetocentric and planetographic longitudes of a point have opposite sign.
Target Position Level 3 [Level_3]
The instructions for this field are identical to those for the Level 2 field except that “Level 3” should be substituted wherever “Level 2” occurs, and “Level 2” should be substituted wherever “Level 1” occurs.