We present below a checklist of steps for measuring photometry of sources on images collected with the WFC3 UVIS and IR detectors. A detailed description of each step is provided in the following sections. 

• Download data products appropriate to your science case from MAST:
  • Single exposures (FLT) or drizzled (DRZ) images
  • CTE-corrected¹ (FLC/DRC) or not-corrected (FLT/DRZ) UVIS images  

• Apply the Pixel Area Map (PAM) correction (only when performing aperture photometry on FLT/FLC images; not needed for surface brightness photometry) 
• Perform Aperture or Point-Spread Function (PSF) photometry according to the science case 
• Apply an aperture correction to the measured count rates if performing PSF photometry or using a small (≤ 5 pixels) aperture radius 
• Apply the WFC3 tabulated encircled energy (EE) corrections to infinity to the aperture corrected count rates 
• Convert the count rates to the appropriate photometric system (VEGAMAG , STMAG, or ABMAG) by using the WFC3 provided inverse sensitivities or zero points 
• Apply count-rate non-linearity correction (IR only, if needed)  
• Check blue leak levels for possible impact (rare, IR only; WFC3 ISR 2008-05)
• Apply a color term correction (UV filters, if needed) 
• Correct for red leak (UV filters, if needed; WFC3 ISR 2008-49) 

Summarizing, after downloading the selected image type, applying the PAM correction if needed, and performing small-radii aperture or PSF photometry on the data, to obtain calibrated magnitudes, M, from the instrumental ones, m, the following equation can be used:

 where $//<![CDATA[ \begin{array}{l}AP_{10}\end{array} //]]>$ is the correction to a 10-pixel aperture radius (recommended), $//<![CDATA[ \begin{array}{l}EE_{inf}\end{array} //]]>$ is the encircled energy correction to infinity,$//<![CDATA[ \begin{array}{l}exptime\end{array} //]]>$ is the exposure time of the image (for UVIS data only), $//<![CDATA[ \begin{array}{l}ZP_{VEGA,ST,AB}\end{array} //]]>$ is the magnitude zero point in the VEGAMAG, STMAG or ABMAG photometric system, $//<![CDATA[ \begin{array}{l}CRNL\end{array} //]]>$ is the count-rate non-linearity correction for the IR detector, and $//<![CDATA[ \begin{array}{l}CT\end{array} //]]>$ and $//<![CDATA[ \begin{array}{l}RL\end{array} //]]>$  are the color term and red leak corrections for UV filters. 

9.1.1 Photometric Systems

The WFC3 filters naturally define their own photometric system and users are encouraged to refer their photometric results to this native system. The natural instrumental magnitude of an object observed in a WFC3 filter is instrumental mag = -2.5 log (count rate), where the count rate is in units of electrons per second (e¯/sec). WFC3 supports the STMAG, ABMAG and VEGAMAG photometric systems and provides zero points for these, in addition to the filter-dependent instrument sensitivity, which converts the measured count rate (e¯/sec) to a mean flux density Fλ in units of erg cm^-2 s^-1 Å^-1 and Fν in units of erg cm^-2 s^-1 Hz^-1.

The STMAG and ABMAG systems define an equivalent flux density for a source , corresponding to the flux density of a source of predefined spectral shape that would produce the observed count rate, and convert this equivalent flux to a magnitude (see e.g. stsynphot). The conversion is chosen so that the magnitude in V corresponds roughly to that in the Johnson system.

In the STMAG system, the flux density is expressed per unit wavelength, and the reference spectrum is flat in F_λ. An object with F_λ = 3.63 x 10-9 erg cm^-2 s^-1 Å^-1 will have STMAG=0 in every filter, where the STMAG zero point is -21.10 (PHOTZPT header keyword).

• STMAG = -2.5 log F_λ - 21.10

In the ABMAG system, the flux density is expressed per unit frequency, and the reference spectrum is flat in F_ν. An object with F_ν = 3.63 x 10^-20 erg cm^-2 s^-1 Hz^-1 will have magnitude ABMAG=0 in every filter, where the ABMAG zero point is -48.6.

• ABMAG = -2.5 log F_ν - 48.6

The relationship between ABMAG and STMAG is:

• ABMAG = STMAG - 5 log (PHOTPLAM) + 18.692

where F_ν is expressed in erg cm^-2 s^-1 Hz^-1, F_λ in erg cm^-2 s^-1 Å^-1, and PHOTPLAM is the bandpass pivot wavelength in angstroms. PHOTPLAM values for all filters are listed in Column 3 of Table 6.2 of the WFC3 Instrument Handbook.

Formally, the HST VEGAMAG system is defined by the absolute spectral energy distribution of Vega, such that Vega has VEGAMAG=0 at all wavelengths. Thus, the VEGAMAG magnitude of an object with flux F is:

• VEGAMAG = -2.5 log (F_object / F_vega) 

where F_vega is the CALSPEC observed flux density of Vega. For the equations that define the average flux, see Bohlin 2014 and Bohlin et al. 2020. In the Johnson-Cousins magnitude system, the average value of six A0V stars sets the zero point values so that U-B=0 and B-V=0 (Johnson & Morgan, 1953) and by extension V-R=0 and V-I =0 (Cousins 1974). In this system Vega has the following magnitudes: U=0.03, B=0.03, V=0.03, R=0.07, I=0.10, J=-0.18, H=-0.03, K=0.13. The VEGAMAG system is convenient for many observers because of its long heritage; however, the ABMAG system is popular with large imaging surveys.

A detailed discussion of these three photometric systems within the context of HST observations is provided in Sirianni et al. 2005 as well as WFC3 ISR 2009-31 and in stsynphot. Further information on the VEGAMAG system is also provided in Bohlin & Gilliland (2004), the ABMAG system in Oke (1964) and the STMAG system in Koorneef et al. (1986). Although convenient, transformation to these (as well as other) photometric systems always has limited precision and is dependent on the color range, surface gravity, and metallicity of the source stars considered (Sirianni et al. 2005). A Jupyter notebook illustrating filter transformations between the WFC3/UVIS photometric system and others is available here (see also Section 9.5.2).

Photometric Zero Points

The photometric zero point of a telescope/instrument/filter combination is a convenient way to characterize the overall sensitivity of the system. By most definitions, the zero point represents the magnitude of a star-like object that produces one count per second within a given aperture (see Maiz Apellaniz 2007). For WFC3, this throughput measures the performance within a given bandpass taking into account the HST Optical Telescope Assembly (OTA), pick-off mirror and relay mirror reflectivity, filter throughput, transmission of the outer and inner detector package windows, and the quantum efficiency (QE) of the detector. For HST instruments such as WFC3, the zero points depend on the absolute flux calibration of HST white dwarf model atmosphere spectra, and therefore they will change whenever that calibration is improved.

The photometric zero point can be determined using several techniques. In stynphot, a photometric and spectral simulator, a user can renormalize a spectrum to 1 count/sec in the appropriate WFC3 bandpass and output the zero point in the selected magnitude system (assuming that updated throughput tables are included in the local synphot installation). A Jupyter notebook illustrating how to calculate WFC3 zeropoints with synphot is also available.

Similarly, the STMAG and ABMAG zero points for WFC3 data can be computed using photometric keywords in the SCI extension(s) of the image header as follows:

ZP_STMAG = -2.5 log (PHOTFLAM) + PHOTZPT = -2.5 log (PHOTFLAM) - 21.10
 
ZP_ABMAG = -2.5 log (PHOTFLAM) - 21.10 - 5 log (PHOTPLAM) + 18.692

where, fits header keyword PHOTFLAM is the inverse sensitivity and represents the flux density (erg cm^-2 s^-1 Å^-1) of a star that produces a response of one electron per second in this bandpass and PHOTPLAM is the pivot wavelength in Angstroms, where pivot wavelength is a measure of the effective wavelength of a filter (Tokunaga & Vacca 2006).

For more information, please see WFC3 ISR 2021-04, Calamida et al. (2022) and the WFC3 Photometric Calibration webpage.   

Photometric Transformations

In some cases it may be desirable to compare WFC3 photometric results with datasets in different photometric systems (e.g., WFPC2, ACS, SDSS, 2MASS, Johnson-Cousins). Since the WFC3 filters do not have exact counterparts in any other “standard” filter set, the accuracy of these transformations is limited. Moreover if the transformations are applied to objects whose spectral type (e.g., color, metallicity, surface gravity) do not match the spectral type of the calibration observation, serious systematic effects can be introduced.

Transformation coefficients for different spectral types and astronomical sources have been published (WFC3 ISR 2014-16). The photometric transformation coefficients between Johnson-Cousins UBVI filters and WFC3 UVIS wide-band filters for a given object spectrum can also be computed.  A WFC3 Jupyter notebook tutorial has been developed to assist users with these computations and is described in Section 9.5.2.

9.1.2 Pixel Area Maps

If one decided to perform photometry (aperture or PSF) on flt/flc images then the data needs to be corrected for pixel area variations in the data array. The WFC3/UVIS CCDs and WFC3/IR detector contain pixels that vary in their area on the sky as a result of the geometric distortion. As a consequence of this, a larger pixel collects more photons relative to a smaller pixel, leading to an overall gradient in an image of an intrinsically uniform background. However, the flat-fielding process in the HST calwf3 pipeline is designed to correct for that gradient and produce images that have a flat background. As a result, while surface photometry measurements on flat-fielded science data (flt) will be correct, the measured total brightness of sources will vary depending on the position of the object i.e. the areas of the pixels underlying the source.

To achieve uniform aperture photometry of point sources over the detector, observers can either use flt/flc images after applying a pixel area map (PAM) correction or use distortion-free images (drz/drc). The AstroDrizzle software corrects for distortion, yielding images (drz/drc) which have a flat sky and contain pixels that are uniform in area (i.e., corrected for distortion and related pixel area variations). Therefore, photometry of any source in an AstroDrizzle (drz/drc) image will yield the same count rate irrespective of the position of the source on the image. Photometry measured on a calibration pipeline image (flt/flc) requires a field-dependent correction factor (PAM) to achieve uniformity in the measured count rate of an object across the field.

This PAM correction, in the form of an image, comes from the derivatives of the geometric distortion polynomial. The size of the PAM image is the same as the calibrated (flt/flc) image and each pixel value is set to the normalized area of that pixel. By multiplying the calibrated (flt/flc) images by the PAM image, users will recover the same count rate on both types of images (flt/flc and drz/drc) and the same zero point will apply to both data products, e.g. drz = flt * PAM, where the (flt/flc) image has been converted to counts per second.

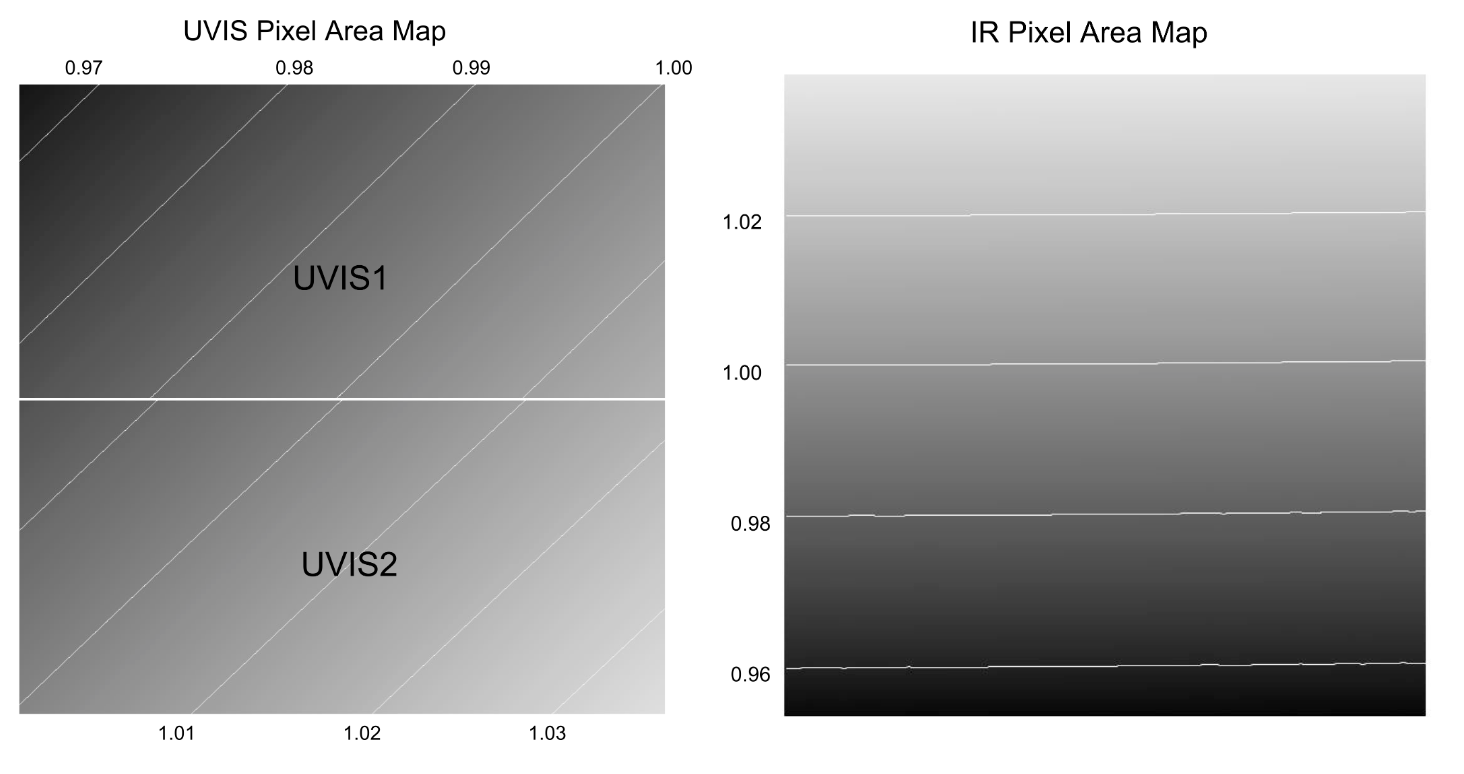
A contour plot of the relative pixel size across the UVIS image, normalized to the central pixel, is shown in the left panel of Figure 9.1; the ratio of maximum to minimum pixel area is 1.074. The variation of pixel area across the IR channel is shown in the right panel of Figure 9.5; the maximum deviation from the central value is 4.1%.

A detailed description of the WFC3 UVIS and IR PAMs is provided in WFC3 ISR 2010-08, which also discusses a unique choice for normalizing the WFC3 PAMs that differs from previous instruments. This approach ensures that the PAM images do not artificially scale the flux in flt/flc images by large amounts. Instead, the PAM images simply serve to provide a relative correction of the counts based on the size of pixels as compared to the size of a reference pixel near the center of the detectors (WFC3 ISR 2010-08).

PAM Concept Illustration

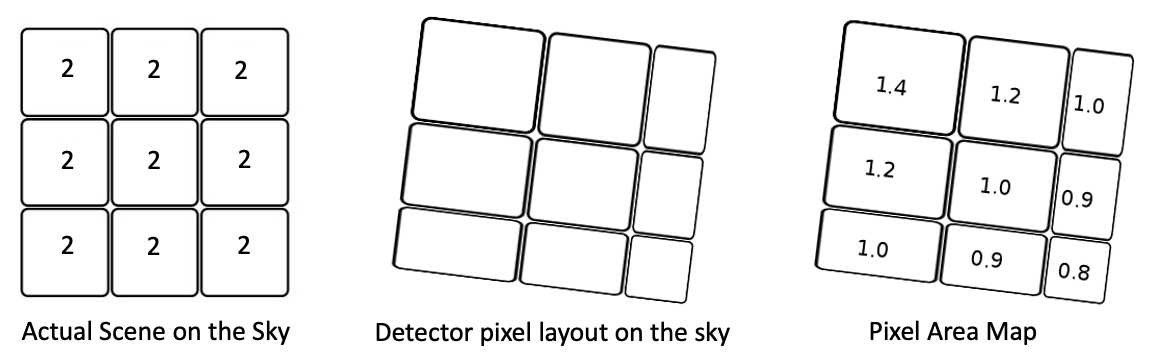
To illustrate the concepts of extended source and point source photometry on images (flt, drz) we consider a simple idealized example of a 3 × 3 pixel section of the detector. We assume that the bias and dark corrections are zero and that the quantum efficiency is unity everywhere.

Example #1 Constant Surface Brightness Object

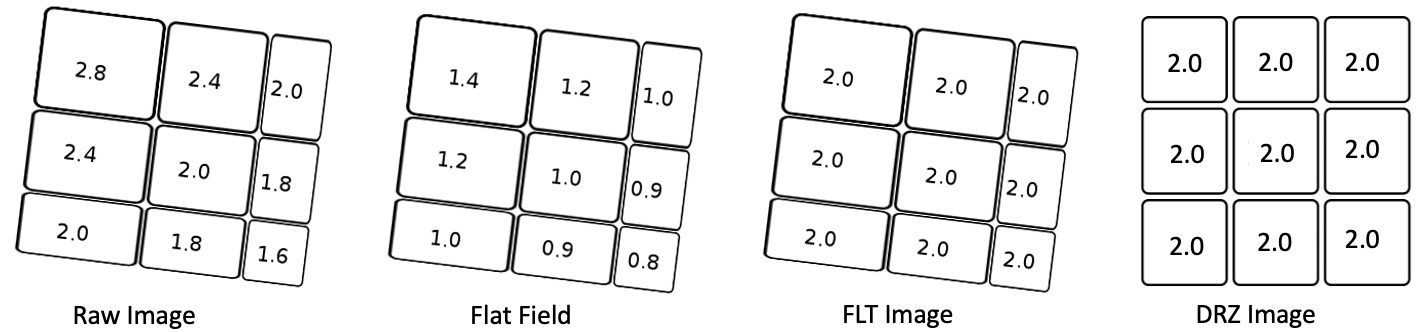
Assume an extended object has a surface brightness of 2 e¯/pixel in the undistorted case. Without any geometric distortion the image is shown in Figure 9.2 as the 'Actual Scene on the sky'. With geometric distortion, the pixels are not square and the pixel area varies across the detector, as shown in the 'Detector pixel layout on the sky', with a corresponding PAM in the top-right panel.

As a result of the distortion, there will be an apparent variation in surface brightness in the raw image (no flat applied). The geometric area of each pixel is imprinted in the flat field as well as the photometric sensitivity. In this example, since we assumed that the quantum efficiency is unity everywhere, the flat field is just the equivalent of the PAM. WFC3 flat fields are designed to level out a uniformly illuminated source and not to conserve total integrated counts, so after the flat-field correction the science image (flt/flc) has the correct surface brightness and can be used to perform surface photometry. However, the image morphology is distorted. AstroDrizzle can be run on the flat fielded image (flt/flc); the resulting image (drz/drc) will have pixels free of geometric distortion.

Example #2 Photometry of a point source

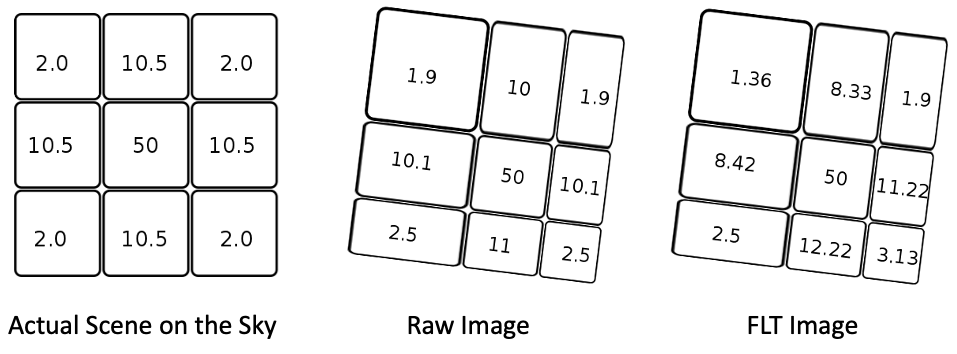
Assume we are observing a point source and that all the flux is included in the 3 × 3 grid with the count distribution as shown in the left panel of Figure 9.3. The total counts are 100. Due to geometric distortion, the PSF as seen in the raw image is distorted, i.e. the total counts are conserved but they are redistributed on the CCD. The flat-field correction, however, does not conserve the total counts since the counts now add up to 99.08, instead of 100. For accurate integrated photometry on flat fielded WFC3 images, the pixel area variation must be taken into account. This can be done by multiplying the science image (flt/flc) by the PAM image or by running AstroDrizzle and performing the photometry on the drz/drc image.

Only by running AstroDrizzle can the geometric distortion be removed, but both approaches (using either drz/drc or flt/flc x PAM) will correctly recover integrated count total as 100. Users should be cautioned that this is just an idealized example. In reality the PSF of the star extends to a much bigger radius. If the user decides to work on the flt x PAM image, they should calculate a new aperture correction to the total flux of the star as the aperture corrections discussed in Section 9.1.8 are only for drizzled output images (drz/drc).

9.1.3 Aperture and Encircled Energy Corrections

In order to reduce errors due to background variations and source crowding, aperture photometry and PSF-fitting photometry are often performed by measuring the flux within a small radius ($//<![CDATA[ \begin{array}{l}\le\end{array} //]]>$ 5 pixels) around the center of the source. However, small aperture photometric measurements need to be adjusted to a 'total' count rate of the source, i.e. to an 'infinite' aperture radius, by applying an aperture correction (in magnitude units) or an Encircled Energy (EE) fraction (in flux units). For example, the measured UVIS flux in the F606W filter within a 10-pixel  (0.4") aperture radius is ~91% of the total flux and within a 50-pixel (2.0") radius aperture is ~98% of the total flux. For the IR detector, the flux in F140W within an aperture radius of 3 pixels is ~84% of the total flux and ~97% within an aperture radius of 15 pixels (2.0"). 

To compute aperture corrections, a two-step process is recommended. First, users should determine the offset between their own small aperture photometry and photometry within a ‘standard’ aperture radius, beyond which the EE does not change due to orbital breathing or detector position. This radius was measured to be approximately 10 pixels for the UVIS and 3 pixels for the IR detector, respectively. Therefore, the recommendation is to correct small aperture and PSF photometry to these radii before applying the EE corrections to infinity. For more details on this procedure please see the WFC3 UVIS and IR EE webpages. 

For the first step, the aperture correction can be calculated by measuring magnitudes or fluxes of a few bright stars in an uncrowded region of the image at the selected small aperture radius and at 10 (UVIS) or 3 (IR) pixel radius and calculating the magnitude difference or flux ratio. These offsets should be applied to the photometric measurements of all sources in the image. If such stars are not available, tabulated EE values for different aperture radii might be applied instead. Alternately, the MAST PSF search tool can be used to download PSFs extracted from WFC3 archival data for a similar detector position and focus as the observation of interest, and if appropriate aperture corrections can be calculated using these. The WFC3 observed PSF database can be accessed by choosing the 'Select a collection' to 'WFC3 PSF' on the MAST Portal interface (for details, see WFC3 ISR 2021-12). There are a total of about 32 million UVIS PSFs (29 unsaturated and 3 saturated) and 25.2 million IR PSFs (25 unsaturated and 0.2 saturated) in all the WFC3 images taken prior to January 2024, and all of these observed PSFs are available through the MAST Portal interface. In order to download appropriate PSFs, the user can first use the HST focus model (the "Annual Summary" provides the model focus values at 5-minute intervals) to estimate the focus value at the time of the observation. Then, the WFC3 PSF database can be searched for PSFs observed under similar focus, detector position, etc. as described in WFC3 ISR 2021-12. 

In the second step, the photometry should be corrected to an ‘infinite’ aperture which encloses all of the light of the source. This filter-dependent correction may be taken from the EE tables, which are derived from high signal-to-noise observations of isolated stars out to large radii. Model EEs have been tabulated for the IR (WFC3 ISR 2009-37) and the UVIS (WFC3 ISR 2009-38) detectors. The IR EEs were derived from deep exposures in the F098M and F160W filters and extrapolated to other wavelengths using an optical model. Chip-dependent, filter-based EE fractions were computed for the UVIS detector and spliced to the 2009 in-flight models at r = 35 pixels (~1.4"). These may be found in WFC3 ISR 2017-14 for radii between 3 and 10 pixels and on the WFC3 photometry web pages for radii up to 50 pixels (~2.0"). The 2017 filter-dependent EE values agree with the 2009 models to ~1% for most filters. However, users should keep in mind that accurate aperture corrections are a function of time and position on the detector.

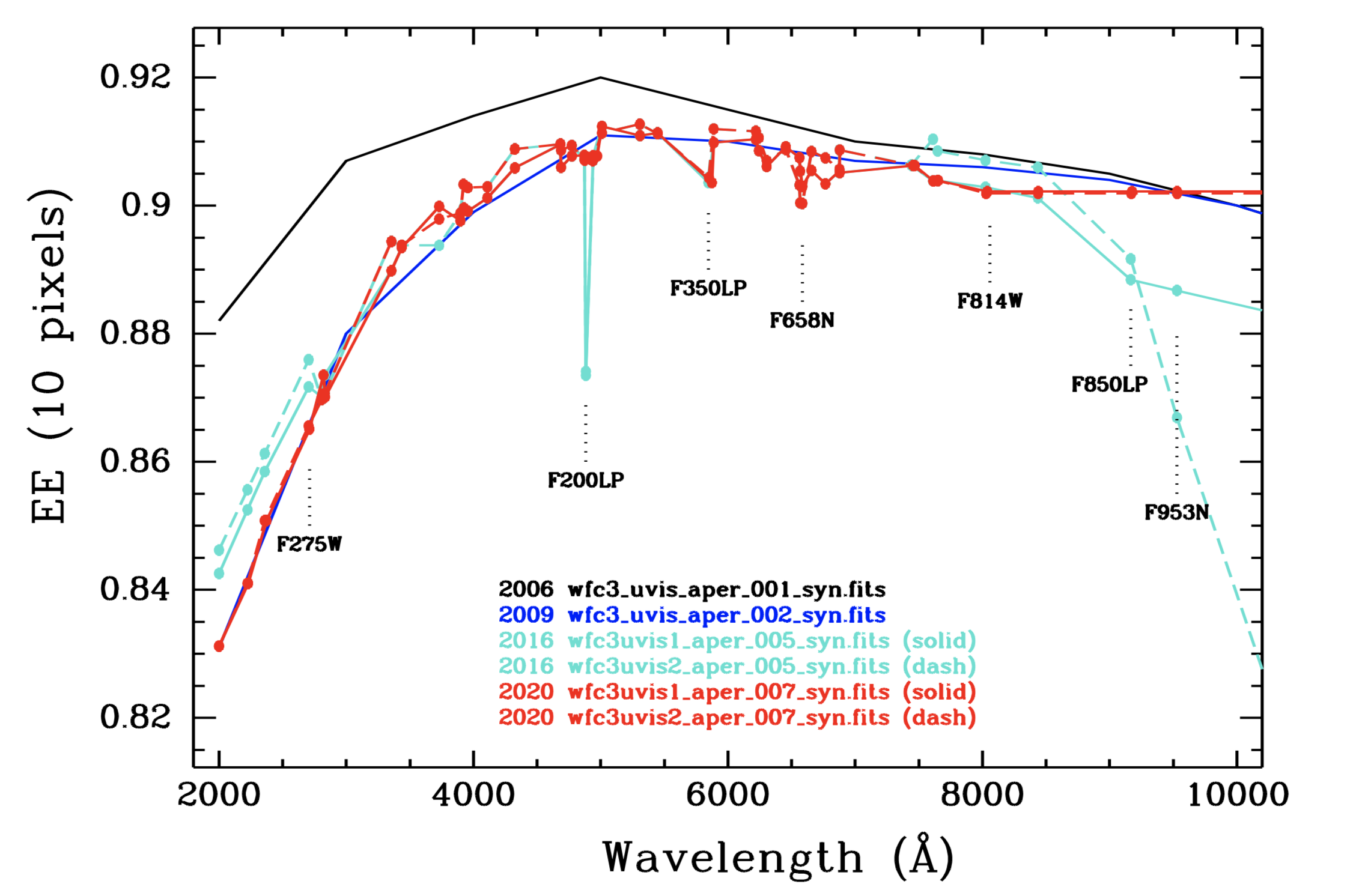
New EE corrections for the UVIS detector were calculated in 2020 for two UVIS filters, F275W and F814W, by correcting for time-dependent sensitivity changes of the detector before stacking the images. Values derived for UVIS1 and UVIS2 showed improved agreement with each other and with the 2009 EE values. Following these results, EE values for the other UV filters were also changed by ~1%. The EE at wavelengths greater than 7,500 Å were changed by ~0.5% to be in close agreement with the F814W values. Figure 9.4 shows the updated EE values at r = 10 pixels (0.3962") as a function of wavelength and compares to prior calibration. For more details, see WFC3 ISR 2022-02.

9.1.4 UVIS Photometric Calibration

The UVIS imaging channel consists of two separate e2v (now Teledyne e2v) CCDs mounted side by side. The two detectors (chips), UVIS2 and UVIS2, have different quantum efficiencies at wavelengths < 3500 Å where UVIS2 is up to ~30% more sensitive than UVIS1 (WFC3 Instrument Handbook Figure 5.2 and WFC3 ISR 2016-03 Figure 1). At longer wavelengths, the response of the two detectors is similar to within 0.5%. Monitoring observations of multiple CALSPEC standards acquired over time show the sensitivity of the two detectors is slowly changing (WFC3 ISRs 2016-17, 2017-15, 2018-16, 2021-04). The count rate ratio of the two detectors also changes with time and shows offsets which vary with the color of the source (see Section 9.1.6).

The absolute photometric calibration of the two UVIS detectors has evolved over the years, including: a single detector solution computed in 2009 and 2012, a chip-dependent calibration in 2016 and 2017, and more recently, a time- and chip-dependent calibration in October 2020 (see WFC3 ISR 2021-04). Any data retrieved from MAST prior to October 2020 can be re-retrieved to obtain the time- and chip-dependent calibration.

When the chip-dependent calibration was implemented, two new header keywords, PHTFLAM1 and PHTFLAM2, were added to the FITS image headers and populated with the inverse sensitivity values for UVIS1 and UVIS2, respectively. For backward compatibility with existing user software, the original header keyword PHOTFLAM was populated with the value of PHTFLAM1. A new keyword switch, FLUXCORR, was also added; this was needed to enable the calibration pipeline, calwf3, to scale fluxes measured on UVIS2 to match those measured on UVIS1 by multiplying the UVIS2 science array by the inverse sensitivity ratio, defined as PHTRATIO = PHTFLAM2/PHTFLAM1 (see Sections 3.2.13 and 3.4.3). After applying PHTRATIO, a source should produce approximately the same number of electrons on UVIS1 and UVIS2 in calibrated (flt/flc) images, corrected for distortion using the pixel area map (see Section 9.1.11). UVIS2 subarray data obtained are also scaled by the PHTRATIO, ensuring that sources have the same count rate in calibrated images, regardless of the chip on which they are observed.

As part of the chip-dependent calibration, updated flat fields were computed for all full-frame filters (excluding the QUAD filters and the grism), with low-frequency corrections for the in-flight sensitivity computed separately for each chip (WFC3 ISR 2016-04, WFC3 ISR 2016-05). The primary change is that the flat fields are normalized separately for each chip and no longer corrected for sensitivity offsets between UVIS1 and UVIS2. Instead, the chip-dependent calibration relies on the FLUXCORR step in calwf3, which uses the inverse sensitivity values in the IMPHTTAB to correct for the chip count rate ratio.

Time-Dependent Solutions

The chip-dependent calibration assumed a constant detector sensitivity with time. As more monitoring data were acquired, small sensitivity changes up to about 0.2% per year were found, depending on the filter and the detector (WFC3 ISR 2018-16, WFC3 ISR 2021-04). Over WFC3's on-orbit timespan to date (2009-2024), the change can amount to about 2%. Differences in the time-dependent sensitivity for UVIS1 and UVIS2, as well as small errors in the flat field between different amplifiers, resulted in count rate ratios across the two UVIS detectors differing by as much as 2% over about 10 years (WFC3 ISR 2018-08, WFC3 ISR 2021-04).

The models for the HST primary spectrophotometric standard white dwarfs (GD153, GD71 and G191B2B) provided by the CALSPEC calibration database were updated in March 2020 (Bohlin et al. 2020). Also, the Vega reference grey flux at 0.5556 μm, as reconciled with mid-IR absolute flux measures from the SPIRIT III instrument on MSX (Midcourse Space Experiment), increased by ~0.9%. The spectral energy distribution for Vega used in the new 2020 calibration is alpha_lyr_stis_010.fits. The standard white dwarf absolute fluxes are determined by the normalization of their modeled spectral energy distributions to their respective relative responses to Vega, using STIS precision spectrophotometry of all three stars along with the flux of Vega at 0.5556 μm (3.47x10-9 erg cm^-2 s^-1 Hz^-1). This method provides the basis for HST's entire calibration system. With the adoption of the new models, the HST primary standard white dwarf absolute fluxes increased overall by ~2% for wavelengths in the range 0.15 - 0.4 μm, and ~1.5% in the range 0.4 - 1 μm, necessitating an update to the WFC3 inverse sensitivities. 

Major changes in the 2020 time-dependent photometric calibration compared to the previous 2017 calibration can be summarized as follows.

1. The latest photometric values are based on updated SEDs for the standard stars and a new reference flux for Vega (Bohlin et al. 2020);
2. Encircled energy (EE) values for a few filters were updated by correcting for the slow changes in sensitivity over time, then re-drizzling the standard star images to compute new EE curves for each chip;
3. Ten additional years of data acquired from 2009-2019 were used;
4. Data from an additional white dwarf spectrophotometric standard (GRW+70d5824) was included in the analysis;
5. Time-dependent corrections were applied to standard star photometry before deriving the inverse sensitivities. Furthermore, the standard star photometric measurements were weighted according to their photometric errors and the number of collected measurements.

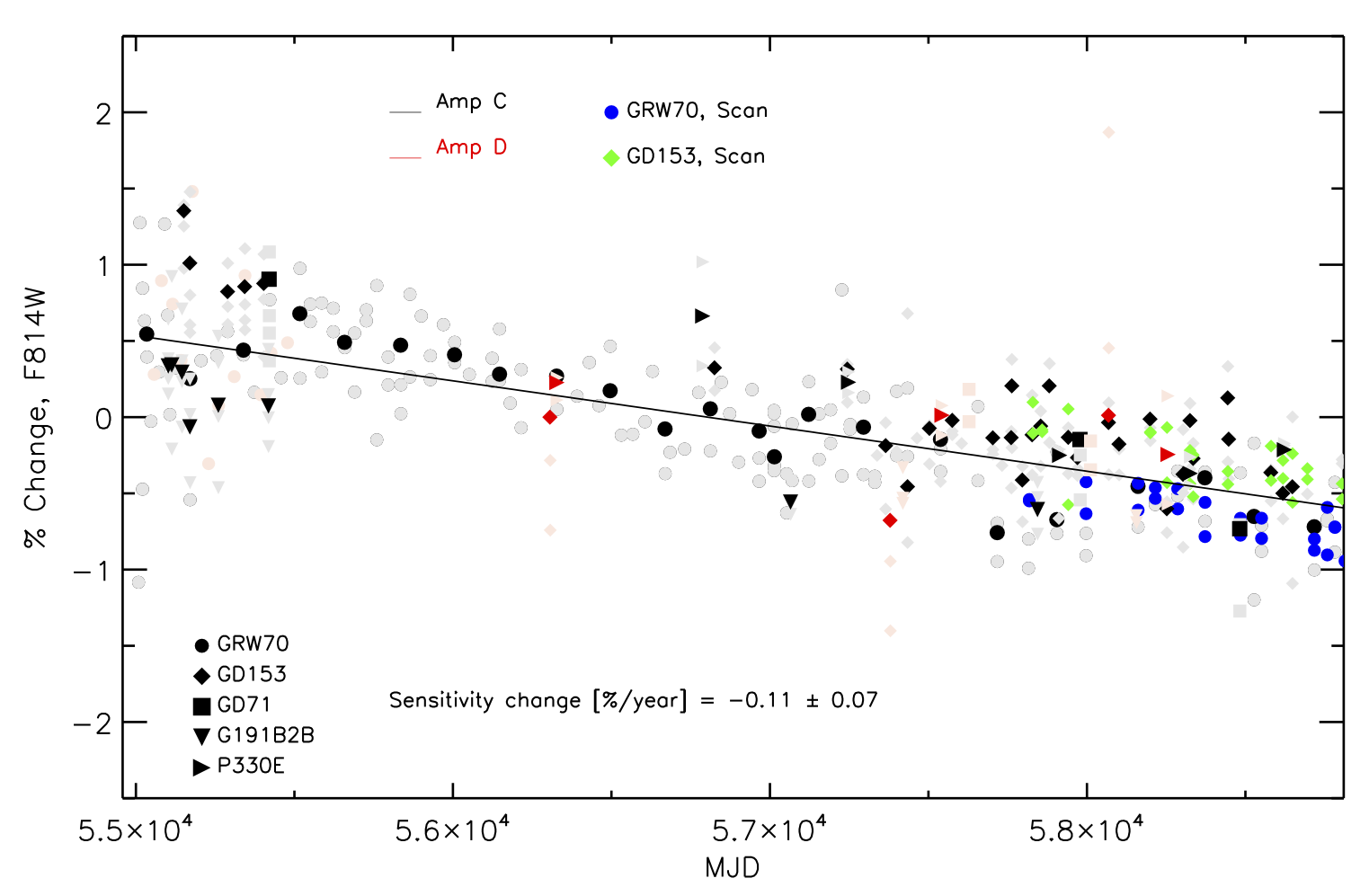
Figure 9.5 shows an example of the time-dependent behavior of UVIS photometry over about 12 years, in this case for UVIS2 and the F814W filter.

The new time-dependent inverse sensitivities provide a photometric internal precision of $//<![CDATA[ \begin{array}{l}\le\end{array} //]]>$ 0.5% for wide-, medium-, and narrow-band filters, with a significant improvement compared to the prior 2016-era values ( $//<![CDATA[ \begin{array}{l}\le\end{array} //]]>$ 1% for wide-, $//<![CDATA[ \begin{array}{l}\le\end{array} //]]>$ 2% for medium-, and $//<![CDATA[ \begin{array}{l}\le\end{array} //]]>$ 5 - 10% for narrow-band filters). The 2020 photometric recalibration is based on an updated correction for the inflight detector response, new encircled energy corrections, and new filter throughput tables for all filters delivered to CRDS. A new image photometry table (IMPHTTAB) was also delivered ('51c1638pi_imp.fits', see Table 9.3) and all WFC3/UVIS archival data were reprocessed through an updated version of the pipeline (calwf3 v3.5.2). The latest models of the spectrophotometric standard stars can be downloaded from the CALSPEC webpage and used in synphot simulations.

The 2020 calibration now ties the inverse sensitivity values to a common reference epoch, i.e. MJD = 55008 (June 26, 2009) for all filters.  Values of the inverse sensitivities for both detectors at each observing epoch can be found in the image header as the PHTFLAM1 and PHTFLAM2 keywords. We also provide a tutorial in Section 9.5.2 for running synphot with the updated filter curves in order to derive the inverse sensitivities, zeropoint values and throughput curves for any detector, observation epoch, filter or aperture. A second tutorial in Section 9.5.2 shows how to use the new time-dependent solutions to work with UVIS data obtained at different observation dates.

Prior UVIS Photometric calibrations

In-flight Calibration in 2009 and 2012

The first in-flight photometric calibration (in 2009) was based on the average measurements of two white dwarf spectrophotometric standard stars (GD153 and GRW+70d5824; WFC3 ISR 2009-31). The total system throughput of both CCDs was found to be significantly better than expected from the Thermal Vacuum 3 (TV3) testing campaign, with efficiency gains of ∼10% at the blue and red ends of the UVIS wavelength range and ∼20% near the central wavelength 5500 Å (Figure 6 in WFC3 ISR 2009-31). A smooth polynomial fit across wavelength was used to correct for the observed increase in on-orbit sensitivity.

By 2012, a larger cumulative set of calibration observations made it possible to replace the polynomial fits with more accurate filter-dependent corrections. These revised solutions were based on the average of three white dwarfs (GD153, GD71, G191B2B) plus the G-type standard star P330E. The revised solutions were not documented in a formal ISR but were posted to the WFC3 photometry web page and populated in the image header keywords PHOTFLAM, PHOTPLAM, and PHOTBW. The updated calibration made use of improved flat fields delivered in 2011 which removed a large internal reflection, known as the UVIS 'flare', and corrected for low-frequency spatial variations in the in-flight sensitivity measured from dithered star cluster observations (WFC3 ISR 2013-10).

Chip-Dependent Solutions

On February 23, 2016, a chip-dependent photometric calibration was implemented for the UVIS detector, and updated inverse sensitivity values were computed (WFC3 ISR 2016-03) and later updated with improved CALSPEC models (WFC3 ISR 2017-14). The inverse sensitivity values were recomputed using calibration observations of only the three spectroscopic standard white dwarfs (GD153, GD71, G191B2B), obtained over about six years and measured at multiple positions on the detector. The 2016 inverse sensitivity values were systematically ~3% smaller than the 2012 set of solutions across the full wavelength range of the UVIS detector and were a result of improvements in the photometric reduction procedure (WFC3 ISR 2016-03). This systematic change, applied retroactively to all UVIS archival data, brought the UVIS photometric system closer to ACS/WFC system (WFC3 ISR 2018-02). 

For prior versions of the inverse sensitivities and EE tables, see Previous UVIS Calibration., and for a summary of prior photometry reference files and synphot tables, see UVIS Calibration History. 

Quad Filters

Updated inverse sensitivities for the 20 UVIS quad filters have been computed using the updated 2020 CALSPEC models for the HST flux standard stars as well as the updated reference flux of Vega (WFC3 ISR 2021-04). The new values do not include any time-dependent correction since insufficient observations were available to reliably measure any changes over time. Aside from the new models, the quad filter photometric calibration is unchanged from 2012 and still makes use of pre-flight (ground) flats that contain the UVIS flare (see Figure 5.4). As a result, the photometric calibration for QUADs filters on amplifier A will have systematic errors of 1 - 2% due this effect. 

The WFC3 UVIS channel contains five quad filters: each is a 2×2 mosaic of filter elements occupying a single filter slot, with each amplifier (quadrant) providing a different bandpass. A subarray observation with a quad filter only covers a single detector quadrant and hence, the science data will have the correct filter keyword reported in their headers. As there is only a single filter keyword in the science image headers, full-frame quad observations always have the filter keyword (FILTER) populated with the quad element that corresponds to quadrant A, regardless of which quad was requested in the Phase II submission. Table 9.1 lists the four spectral elements associated with a single quad element, where the value of the filter keyword reported in the image header corresponds to amplifier A. Users can instead query the value of the “ASN_ID” keyword in the image header and search for that association in MAST, where the archive database is populated with the correct ‘FILTER’ keyword. This discrepancy is due to different software systems creating the MAST database and populating the science image header keywords.

To avoid problems with using PHOTFLAM values from the wrong quadrant, all observations using QUAD filters have the PHOTCORR and FLUXCORR switches set to OMIT. As a result, the photometric keywords are not populated in the image header during calwf3 processing. The PHOTFLAM values thus have to be retrieved elsewhere, for example from Table 7 in WFC3 ISR 2021-04 or from the quad filter tables on the photometry website.

Table 9.1:  Detector quadrant (amp) imaging locations for the WFC3 quad filters. 

9.1.6 UV Filters

Photometric Calibration

One motivation of the chip-dependent calibration described above was to quantify and correct for bandpass differences, i.e. the response functions, between the two detectors in the UV. Even when two systems (telescope + UVIS1 or UVIS2) use the same filter, due to chip QE differences, the effective bandpass is different in the UV (WFC3 ISR 2017-07, WFC3 ISR 2018-08, WFC3 ISR 2021-04).

Calibrated WFC3 data products (*flt.fits, *flc.fits) are combined in the pipeline using the AstroDrizzle software to create distortion-free data products (*drz.fits, *drc.fits) with the two CCD chips drizzled to the same output frame. AstroDrizzle assumes the images are in units of counts or count rate and not in the flux units used for photometry. This means that the same source must have the same count rate on both chips for AstroDrizzle to properly combine dithered data in which the same sources fall on both chips. Because of the different effective bandpasses in the UV, the measured count rate ratio between chips for the white dwarf standards does not equal the PHTRATIO value provided in the 2016 IMPHTTAB ('z*imp.fits') for the UV filters. 

Therefore, on November 21, 2016, the photometric calibration of the UV filters was improved by the delivery of a revised IMPHTTAB ('0*imp.fits'), which scales the PHTFLAM1 values by a factor reflecting the empirical count rate ratio of the white dwarf standards. These modified values of PHTFLAM1 are provided for the four UV filters (F218W, F225W, F275W and F200LP), such that the PHTRATIO values in the image header match the observed count rate ratios for the white dwarf standards. In this case, the PHOTFLAM value should be used to perform flux calibration, and not PHTFLAM1, which has been modified to normalize the count rate ratio.

For programs which require very precise (< 1%) photometry in the UV filters, users are advised to treat the two chips as separate detectors and use the chip-dependent keyword values to perform the flux calibration, PHTFLAM1 and PHTFLAM2. For UVIS1, this means simply multiplying the measured count rates by PHOTFLAM (which is equal to PHTFLAM1). For UVIS2, the science array has already been scaled by PHTRATIO, so flux calibration may be achieved by dividing the measured count rates by PHTRATIO and then multiplying by PHTFLAM2, as reported in the image header. In this case, photometry can be computed directly from the calibrated data products (*flt.fits, *flc.fits) multiplied by the pixel area map to account for geometric distortion. Alternately, users can correct for variations in the pixel area by drizzling each chip separately prior to performing photometry. This makes it easier to keep track of which inverse sensitivity value to use with which detector pixels, of particular importance for observations obtained at different orientations or with large dithers.

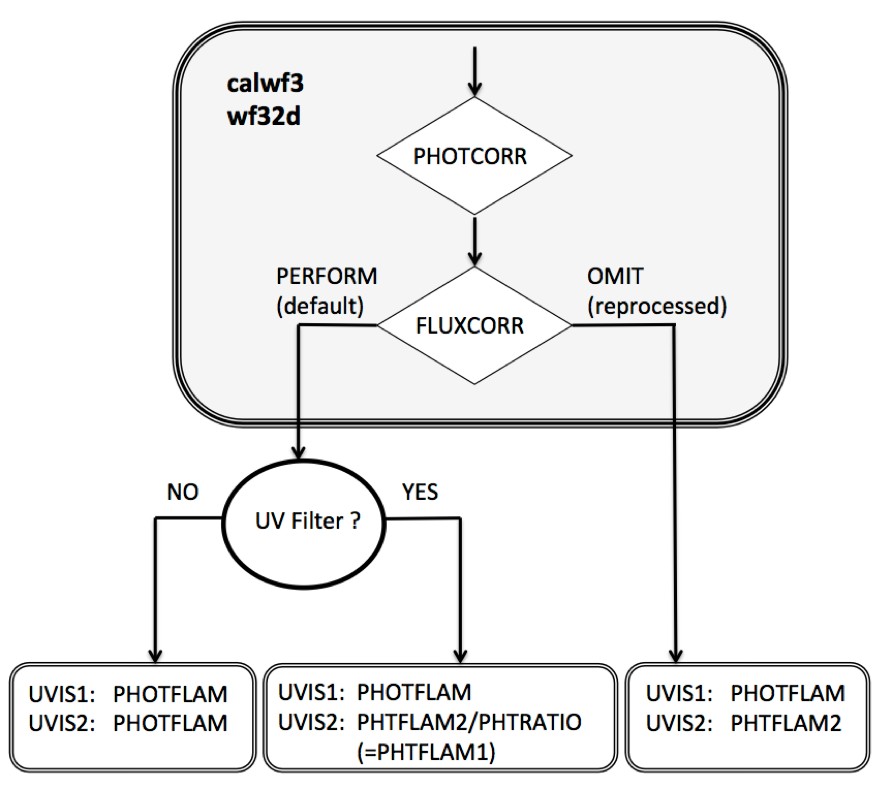
A flowchart for determining which photometric keywords to use for photometry with UV filters is provided in Figure 9.6. The light gray box shows the final calwf3 processing steps in the wf32d module. The data products (*flt.fits, *flc.fits) obtained from MAST are created with FLUXCORR set to PERFORM in calwf3. Subsequently, the header keyword PHOTFLAM, i.e. a unique inverse sensitivity value, can be used to perform the flux calibration of both chips. For the UV filters F218W, F225W, F275W, F200LP, bandpass differences between the two chips results in the count ratio not being equal across them. In order to combine the two chips to create the drizzled (*drz.fits, *drc.fits) data products, calwf3 multiplies the UVIS2 science array by PHTRATIO (the inverse sensitivity ratio) to bring both chips on the same flux level. Hence, using a single PHOTFLAM value for both chips may lead to errors of up to 2% in these filters (WFC3 ISR 2017-07) since the measured count rate ratio between chips for the white dwarf standards does not equal the PHTRATIO value provided in the IMPHTTAB. To achieve high photometric precision (< 1%) in these UV filters, users are advised to treat the two chips as independent detectors. This is accomplished either by using an alternate set of keywords (bottom center) or by setting FLUXCORR to OMIT, reprocessing the RAW (*raw.fits) data with calwf3, and using a third set of keywords (bottom right).

Color terms

The UVIS1 and UVIS2 detectors have different quantum efficiencies in the ultra-violet (UV) regime (λ < 4,000 Å), where count rate ratios change as a function of spectral type. When calibrating photometry of stars cooler than T_eff ~ 30,000 K in the UV filters (e.g. when observing open and globular clusters, resolved local group galaxies, Galactic stellar populations), color term transformations must be applied to UVIS2 magnitudes. Sources of any spectral type observed only on a single UVIS detector will not require any magnitude offset.

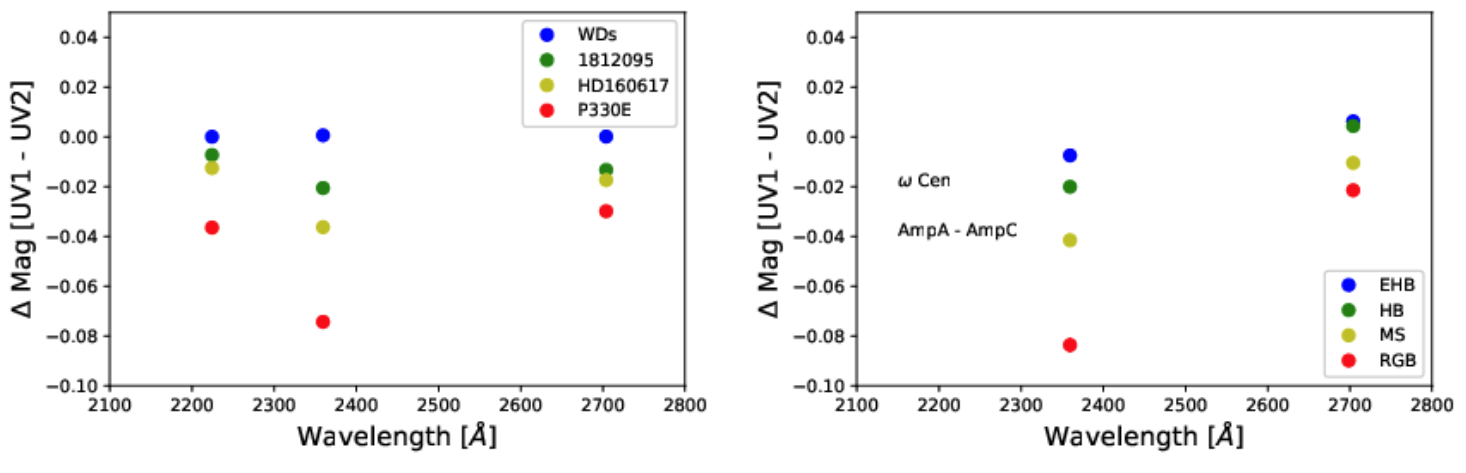
The upper panel of Figure 9.7 shows the synthetic ST magnitude difference, UVIS1 – UVIS2, for a sample of CALSPEC standard stars of varying spectral type (the white dwarfs (WDs) include G191B2B, GD71 and GD153), as computed for the three UV filters F218W, F225W, and F275W. Note that cool red sources such as the G-type star P330E measured on UVIS2 have a magnitude offset relative to UVIS1 up to ~0.08 mag when observed with the F225W filter while F-type stars such as HD160617 have a magnitude offset of ~0.04 mag.

The lower panel of Figure 9.7 shows the ST magnitude difference for the F225W and F275W filters for ω Cen Extreme Horizontal Branch (EHB), Horizontal Branch (HB), Main Sequence (MS), and Red-Giant Branch (RGB) stars measured on different detectors and amplifiers, A (UVIS1) and C (UVIS2). WFC3 observations of ω Cen validate the results of synthetic photometry: red stars (RGBs) observed on UVIS2 have a magnitude offset up to 0.08 mag relative to UVIS1.

Lookup tables with color term transformations are provided in WFC3 ISR 2018-08. The corrections may be applied to UVIS2 magnitudes when observing with the three UV filters F218W, F225W, and F275W. 

Before applying the offset to magnitudes measured on UVIS2, photometry must first be calibrated using the UVIS1 inverse sensitivities:

ZP_STMAG (UVIS1) = -2.5 log (PHOTFLAM) - 21.1
ZP_STMAG (UVIS2) = -2.5 log (PHOTFLAM) - 21.1 + Delta (Mag)

where the Delta (Mag) = Mag(UVIS1 – UVIS2) correction is listed in lookup tables in WFC3 ISR 2018-08.

Red Leak

The design and manufacture of the UV filters was based on a careful balance of the achievable in- and out-of-band transmissions. In general, higher in-band transmission results in poorer suppression of out-of-band transmission, and vice versa. The WFC3 filters represent an attempt to achieve an optimum result, maximizing the in-band transmission while keeping the out-of-band transmission as low as possible in order to minimize red leaks.

Table 9.1 below summarizes the red-leak levels for the WFC3 UV filters based on the results in WFC3 ISR 2008-49. The table lists the fraction of the total signal that is due to flux longward of 400 nm, as a function of effective temperature, calculated by convolving a blackbody of the given effective temperature (T_eff) with the system throughput in the listed filter. As can be seen from the table, red leaks should not be an issue for observations of any objects taken with F275W or F336W. The other UV filters have some red leaks, whose importance depends on stellar temperature. The red leaks in F218W and F300X, for example, exceed ~1% for objects cooler than ~6000 K, while in F225W the red leak reaches ~1% for objects with even cooler temperatures. The most extreme red leaks arise from F218W and F225W observations of objects with effective temperature (T_eff) of ~4000 K or cooler, necessitating appropriate corrections.

Table 9.1: Fraction of flux longward of 400 nm as a function of effective temperature.

Contamination

The UVIS detector is regularly monitored for contamination effects i.e. a decline of sensitivity which could be due to volatile molecules accumulating on either the detector itself or on other optical surfaces. When present, contamination is expected to manifest as a wavelength-dependent decline in the photometric throughput, i.e. with the strongest effect present in the bluest filters. Historically, contamination monitoring has been done via observations of the spectrophotometric white dwarf standard GRW+70d5824 in several key filters from 200 nm to 600 nm, with red filters acting as a control (WFC3 ISR 2011-18, WFC3 ISR 2014-20). In late 2015, a second white dwarf standard star, GD153, was added to the monitoring program (WFC3 ISR 2017-15). In addition, scanning-mode observations of two standard stars were added to improve the precision of relative photometry over time (WFC3 ISR 2017-21). WFC3 ISR 2021-04 shows that spatial scan measurements are more precise than staring mode ones: scans have ~ 2.5 less residual noise than their staring mode counterparts (see WFC3 ISR 2022-04).  

For scans, sensitivity losses are relatively flat independent of wavelength on both UVIS detectors, with no evidence of contamination. UVIS2 appears to have slightly higher losses (-0.17+/- 0.01 %/yr) compared to UVIS1 (-0.12+/-0.01 %/yr). When measured over the same time period, spatial scans and staring mode observations yield filter-dependent loss rates that agree well with each other in most filters within computed uncertainties (WFC3 ISR 2021-04). 

9.1.6 IR Photometric Calibration

For the IR detector, the initial on-orbit photometric calibration in 2009 was based on the average of two CALSPEC spectrophotometric standards (GD153 and P330E, a hot white dwarf and G-type star, respectively). Following the same procedure used for UVIS, a smooth polynomial fit was used to correct for the increase in on-orbit sensitivity with wavelength relative to pre-launch ground tests (WFC3 ISR 2009-30). By 2012, a larger cumulative set of calibration data allowed for more accurate filter-dependent corrections to the sensitivity and the revised solutions were based on the average of three white dwarf standards (GD153, GD71, G191B2B) plus the G-type star (P330E). While these 2012-era solutions were not documented in a formal ISR, they are available from the WFC3 photometry webpage. Independent calibrations from the four standards agree to within ~1% for most wide- and medium-band filters, and the inverse sensitivity per filter (PHOTFLAM) is set to the average of the measurements. 

In October 2020, an updated set of inverse sensitivities was calculated and delivered, using the same data from the 2012 calibration plus 8 additional years of monitoring for the same four standard stars plus the white dwarf GRW+70d5824 (WFC3 ISR 2020-10). The new photometric calibration also included updates to the flat field reference files described in Section 7.8.3 as well as updates to the CALSPEC models. These new model spectra of the standard stars changed their flux, and thus the resulting inverse sensitivities, by approximately 1.5% in the IR (Bohlin et al. (2020); Section 9.1.3). Observers with data retrieved prior to October 2020 can re-retrieve their data to obtain the most up-to-date calibration.

Current estimates of the photometric internal precision of the inverse uncertainties are ~1% for wide-, medium-, and narrow-band filters. A discussion on the photometric errors of the IR detector is provided in Section 7.11. The IR photometry header keywords are populated by calwf3 using the IMPHTTAB reference file, which is described in Section 9.1.7.

Time-dependent solutions

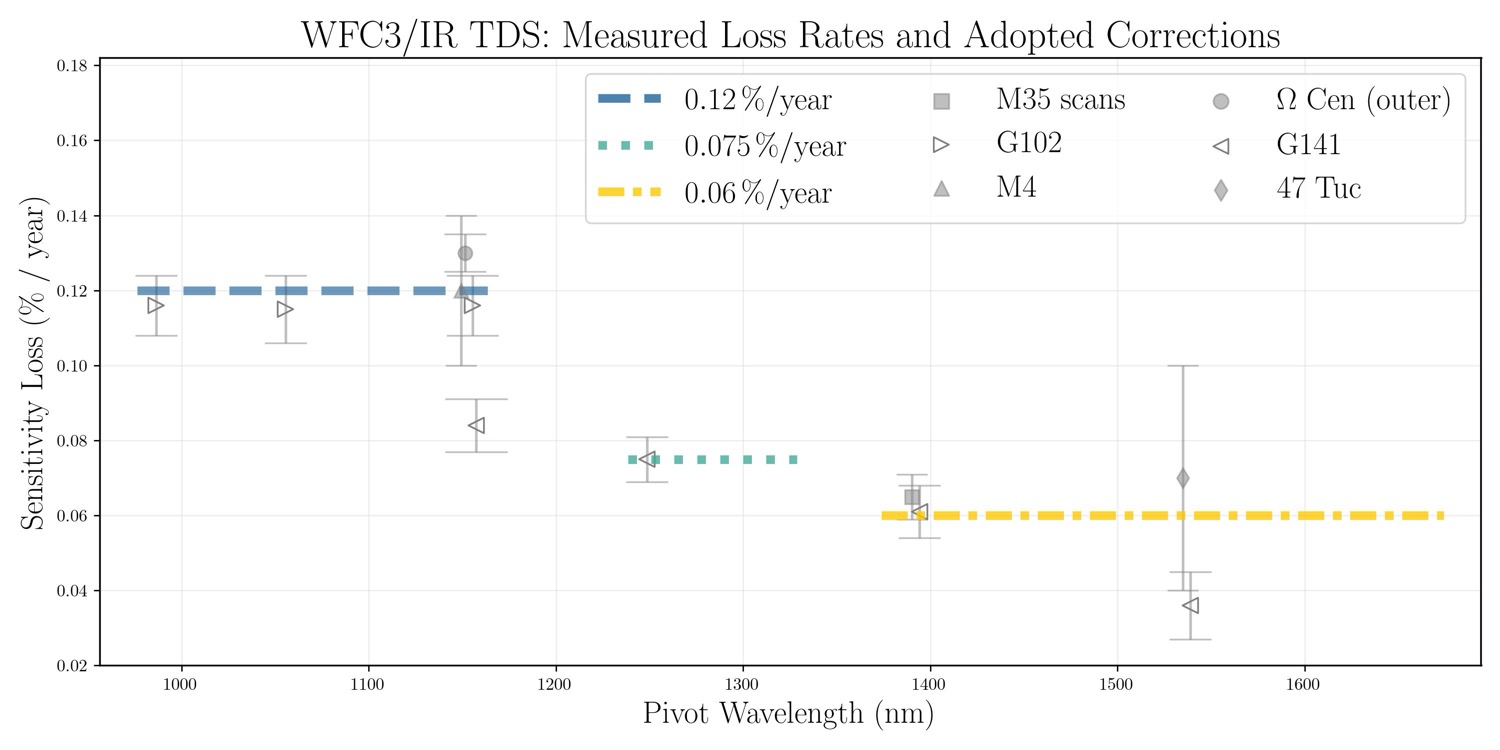
Photometry of fields centered on external (uncrowded) regions of Galactic globular clusters indicated time-dependent sensitivity losses for WFC3/IR. From F160W stare mode imaging of 47 Tuc, the rate of sensitivity loss was measured to be -0.07 ± 0.01 %/yr ; for F110W, changing sensitivity was measured to be -0.12 ± 0.02 % /yr from M4, and 0.13 ± 0.005 %/yr from Omega Centauri (WFC3 ISR 2024-06). These results agree well with those obtained by analyzing spatial scan observations of stars in the open cluster M35 in two filters (WFC3 ISR 2024-01): a sensitivity loss at the rate of -0.065 ± 0.006 %/yr in F140W and -0.157 ± 0.021 %/yr in F098M. Similar loss rates are also seen in integrated grism observations of spectrophotometric standard white dwarfs, with an average sensitivity loss of 0.115 ± 0.008 %/yr in G102 and 0.061 ± 0.007 %/yr in G141. Figure 9.8 presents the stare and scan mode results; for more detail see WFC3 ISR 2024-01. 

Summarizing, the sensitivity loss of the IR detector appears to be wavelength-dependent, with the greatest losses in the bluest filters. The rates of sensitivity loss as a function of pivot wavelength measured by using the different methods discussed are shown in Figure 9.8, with the recommended correction factors plotted as colorful dashed lines that span the pivot wavelengths of the filters for which they are recommended.  

Currently, these slopes must be manually applied by users correct their photometry as described in WFC3 ISR 2024-06. A new image photometry reference table (IMPHTTAB) with these time-dependent inverse sensitivities will be incorporated into the automated calibration pipeline later in 2024.  

Count Rate Non-Linearity

The IR detector exhibits a low-level count rate non-linearity (CRNL) at ~1% per dex over a range of 12 magnitudes (see Section 7.7). Since bright standard stars (11th magnitude) are used to calibrate the detector, this means that faint source photometry (about 23rd magnitude) using the computed set of IR zero points will be systematically ~4.5% too faint and require manual correction (WFC3 ISR 2010-07 and WFC3 ISR 2011-15).  

Additional data to further quantify and correct for this effect as a function of wavelength were obtained in 2016-2017 (calibration programs 14868 and 14870). WFC3 ISR 2019-01 shows results based on these data and on photometry for a set of faint (V ≥17 mag) spectrophotometric standard DA white dwarfs (the White Dwarf Flux Standards, WDFSs, Axelrod et al. 2023). The measured CRNL is 0.0077 +/-0.0008 mag/dex, characterized over 16 magnitudes with no apparent wavelength dependence.

9.1.7 Image Photometry Reference Table

After December 2012 (calwf3 version 3.1.6 and higher), the HST calibration pipeline software (HSTCAL) no longer invoked synphot to calculate the photometric keyword values on-the-fly. Instead, it uses an image photometry lookup table (IMPHTTAB) for each WFC3 channel which contains the values for PHOTFLAM (the inverse sensitivity), PHOTPLAM (the filter pivot wavelength), and PHOTBW (the filter bandwidth). The active IMPHTTAB reference files are listed in Table 9.2 for the UVIS and IR channels and include the latest photometric calibration.

The UVIS chip-dependent calibration implemented in calwf3 v3.3 required a new 5-extension IMPHTTAB reference file to carry additional keywords reflecting the inverse sensitivity for each CCD chip, PHTFLAM1 and PHTFLAM2. When UVIS time-dependent calibration was implemented in calwf3 v3.5.2, the IMPHTTAB was updated to contain additional columns to specify the inverse sensitivity as a function of date (MJD) for each CCD chip.

If data from multiple-visit programs are retrieved from MAST at different times (e.g. after the execution of each visit), there may be systematic differences due to changes in the reference files and/or software. In this case, users have two options: 1) retrieve all pertinent datasets for the given science program from MAST again; 2) reprocess the RAW files offline with a self-consistent version of calwf3 and reference files. For manual reprocessing instructions, see the examples in Section 3.5.

Table 9.2: The IMPHTTAB reference file used to populate the photometry keywords in the image headers of UVIS and IR data. For a history of previous calibration reference files, see the WFC3 Photometry Webpage. 

9.1.8 Narrow-Band Filter Calibration for Emission-Line Objects  

WFC3 has several narrow-band filters which are often used to study emission-line objects like planetary nebulae and HII regions. To derive the emission-line fluxes in such cases, one must correct the observed flux for signal arising from contaminating lines and the underlying continuum. A detailed method to carry out this correction is described in Appendix A of O’Dell et al. (2013). 

¹ The WFC3 UVIS detector suffers degradation of their charge transfer efficiency (CTE), the effect of which is reducing the apparent brightness of sources. There is evidence for CTE degradation over time (see Section 6.3), and this can be mitigated by using either a pixel-based model (Section 6.4), or an empirical correction (Section 6.5).