9.6 Exposure-Time Examples

In the following you will find a set of examples for the three different channels and for different types of sources. The examples were chosen in order to present typical objects for ACS and also to present interesting cases that may arise with the use of ACS.

9.6.1 Example 1: WFC Imaging a Faint Point Source

What is the exposure time needed to obtain a signal-to-noise of 10 for a point source of spectral type F2V, normalized to V = 26.4 in the Vega system, when using WFC and the F555W filter? Assume a gain of 2 e^-/DN, a box size of 11 × 11 pixel², and average sky values.

The ETC gives a total exposure time of 4272 seconds to obtain this S/N in a single exposure using a Castelli and Kurucz spectral model. Since such an exposure would be riddled with cosmic rays and essentially useless, it is necessary to specify how many exposures to split the observation into. ACS WFC observations generally should be split if the exposure time is larger than about 11 minutes, but for multi-orbit observations, splitting into 2 exposures per orbit is generally sufficient.

For a typical object visibility of 53 minutes, after applying the requisite overheads (see Chapter 8), there is time for two 1200 second exposures per orbit. The required exposure time can thus be reached in 4 exposures, but re-running the ETC using # Frames = 4 raises the required exposure time to 4913 seconds (because of the extra noise introduced by the four extra readouts). To achieve the required exposure time would require # Frames = 5, or three orbits.

Using the pencil and paper method, Table 9.1 gives $//<![CDATA[ \begin{array}{l}\int QTd\lambda/\lambda = 0.0768\end{array} //]]>$, and the AB_V correction term can be retrieved from Table 10.1 as 0.01. According to Figure 5.13, a circular aperture of radius 0.3 arcseconds (which has an area of 116 pixels, close to the 121 pixel box specified) encloses about 88% of the light from a star.

The count rate is given by Equation 8 in Section 9.2.1:

which agrees reasonably well with the ETC-returned value of 0.466.

The exposure time can then be found by using Equation 3 in Section 9.3.1, which gives t = 4167 seconds, which is close to the ETC-derived value of 4272 seconds (# Frames = 1). We have inserted the background rate from Table 9.1 (B_sky =  0.0541) and Table 3.1 (B_det = 0.0153), and assumed that the noise from the background is much greater than the readout noise.

Note that this can be greatly shortened by specifying a smaller analysis box (for example, 5 × 5) and using LOW-SKY. Dropping the aperture size to 5 × 5, which still encloses 80% of the light, requires 1426 seconds at average sky. Including both the smaller 5 × 5 box and LOW-SKY (Zodiacal = LOW, Earthshine = AVERAGE), using the ETC gives the required exposure time as only 1230 seconds with # Frames = 1, or 1405 seconds with # Frames = 2. The LOW-SKY visibility per orbit is 47 minutes, which allows a total on-target exposure time of 2000 seconds in one orbit with # Frames = 2.

9.6.2 Example 2: SBC Objective Prism Spectrum of a UV Star

What is the peak count rate using the PR110L prism in the SBC for the HST standard star HS2027+0651 (V = 16.9) that was used for the STIS prism calibration? This spectrum is not in the ETC list, therefore we quote below the flux which can be found by downloading the STIS spectrum from MAST.

The sensitivity peaks in the 1500 Å to 1600 Å region. To find the count rate at 1537 Å, inspection of Figure 6.22 gives the sensitivity of 7.7 × 10¹⁴ counts/second/(erg/cm²/s/Å). Multiplying by the stellar flux of 5.3587 × 10^–14 gives 41.3 counts/second, summed in the cross dispersion direction. For the fraction of light in the central pixel ε = 0.31 (Table 9.2), the brightest pixel at 1537 Å is 12.9 counts/second/pixel, well below the bright object limit.

The SBC has no readout noise, and the dark current rate is negligible, while the main sky contribution for PR110L is from Lyman-α. For daytime Lyman-α intensity of 20kR = 6.1 × 10^–13 ergs/cm²/second/arcseconds² (taken from Table 9.5), S′ =  1.81 × 10¹⁴, and d, the dispersion in Å/pixel, is 2.58. Therefore, the background count rate is given by Equation 3 in Section 9.4.2:

This value varies somewhat over the field, as the plate scale varies from the nominal 0.032 arcseconds/pixel. For faint source spectroscopy, it is better to use PR130L, which is on a CaF₂ substrate to block Ly-α.

9.6.3 Example 3: WFC VIS Polarimetry of the Jet of M87

What signal-to-noise ratio is reached in three one-orbit exposures (~2400 seconds each) for M87 when using WFC/F555W and one of the three VIS polarizers in each orbit? Gain is 2, box size is 5 × 5 pixel², # Frames = 2, and average sky.

If the M87 jet region has μ_V = 17 magnitudes/arcseconds², using the ETC with a flat continuum spectral distribution and an exposure time of 2400 seconds split into two frames, gives S/N = 319 for an observation with each VIS polarizer filter (which is an average of the polarizer at the 3 available position angles 0°, 60°, and 120°). If the polarization P is 20%, then P × S/N = 63.8, so using Equation 6 in Section 6.1.2, σ_P/P  = 0.013, or σ_P  = 2.6 × 10^–3, which is the error on the fractional polarization. The error on the position angle, σ_θ, is 0.4° using Equation 7 in Section 6.1.2.

9.6.4 Example 4: SBC imaging of Jupiter's Aurora at Lyman-alpha

What signal-to-noise ratio is reached in a one orbit exposure (2000 seconds) observing Jupiter's aurora in Ly-α using the SBC and F122M filter?

Equation 10 in Section 9.2.1 can be used to calculate the expected count rate. The aurora is variable, up to ~100kR. The value of (QT) for the SBC/F122M filter at 1216 Å is 0.0122, from inspection of Figure 10.104 and checking the throughput of the bandpass with pysynphot. For a surface brightness of 40kR = 1.22 x 10^–12 erg/cm²/second/arcseconds² (see Section 9.4.2 for conversion), the total counts per pixel are

The background contributions are the detector dark of 8.52 x 10^–6 counts/pixel/second (which can be ignored in this case) and a sky background which is dominated by geocoronal Lyman-α. Using the same formula listed in Example 9.6.2, Equation 3 in Section 9.4.2, we compute the geocoronal background from Lyman-α in the F122M bandpass. During the daytime, the geocoronal background count rate is 0.022 counts/second/pix, while at night the value drops to one tenth of this, or 0.0021 counts/second/pix. After 2000 seconds of integration, the Lyman-α background is 42.3 counts/pix and 4.23 counts/pix for day and night, respectively. 

Finally, we calculate the signal-to-noise ratio Σ for a 2 × 2 pixel² resolution element. In the daytime,

and at night,

9.6.5 Example 5: Coronagraphic imaging of the Beta-Pictoris Disk

In this example, using the now inoperative HRC, we shall consider the case where we are trying to determine the S/N achieved on the Beta Pictoris disk, assuming a disk surface brightness of 16 magnitudes/arcseconds² in the R band at a distance of 6 arcseconds from the central star with a V magnitude of 3.9, for an exposure time of 1000 seconds with an F435W filter. Assume that the star and disk have an A5V-type spectrum. Using the ETC and considering the case for the 3.0 arcseconds occulting mask:

• Disk count rate = 4.98 e^–/second for a 2 × 2 pixel² aperture (including 47.5% throughput of coronagraph).
• Sky count rate = 0.010 e^–/second/pixel.
• Detector dark rate = 0.012 e^–/second/pixel.
• In 1000 seconds, this gives 4,980 e^–/(2 × 2 pixel²) aperture in the disk region.
  
• Central star count rate = 3.63 × 10⁸ e^–/second in a 101 × 101 pixel² aperture (101 × 101 pixel² aperture used to estimate total integrated flux).
  
• At a distance 6 arcseconds from the central star, the fraction of flux per square arcsecond in the PSF wings is 2.6 × 10^–6.  B_PSF = (3.63 × 10⁸) × (2.6 × 10^–6) = 943.8 e^– per square arcsecond. The counts collected in 4 pixels are 4 × 0.027² × 943.8  = 2.752.
  
• The S/N in a 2 × 2 pixel² box is then $//<![CDATA[ \begin{array}{l}\Sigma = \frac{4980}{\sqrt{4980 + 2.8}} = 70.5\end{array} //]]>$.
  

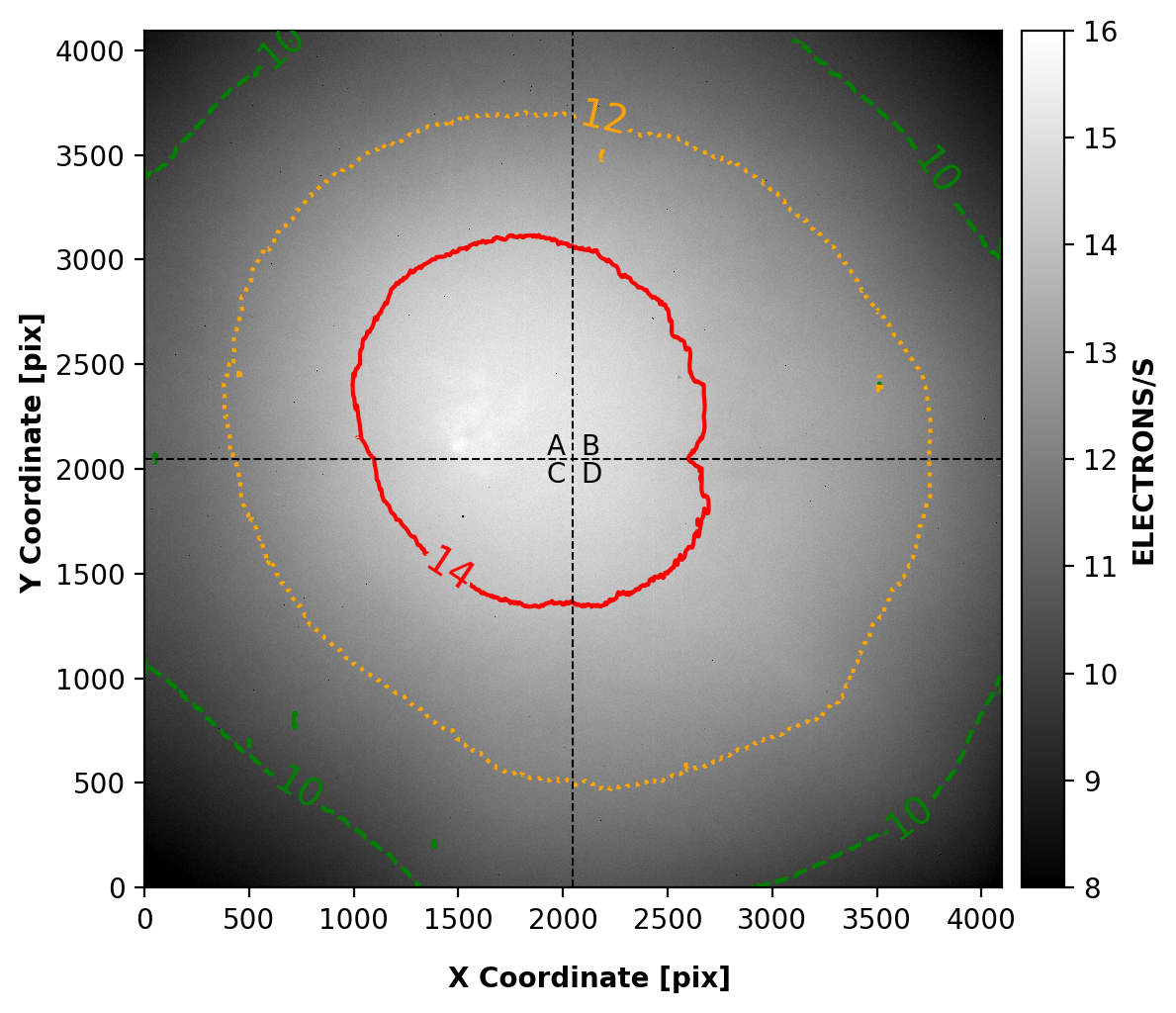
9.6.6 Example 6: WFC Imaging: Post-Flash to Mitigate Low Sky

WFC images with low background (below ~30 e^–/pixel of sky plus dark current) suffer increasingly severe CTE losses far from the serial registers. In some cases, it may be advantageous to post-flash such images to improve recovered signal-to-noise. In the following ETC example, we incorporate post-flash to boost the background for a single 90-second exposure with filter F850LP and "average" levels for earthshine, zodiacal light, and airglow.

We configure the ETC to calculate the S/N ratio obtained in 90 seconds with WFC using the F850LP filter in a single exposure. The ETC also reports the background level as usual. For this example, the flux of the target is irrelevant. Adopting a photometry region of 1 × 1 pixel² for simplicity, and otherwise using default settings, the ETC results page includes a low-background warning (currently triggered below 30e^– per pixel of sky plus dark current) near the top of the report. In this example, the expected background level is only 4.90e^–/pixel (3.52e^– from the sky and 1.38e^– from dark current).

Depending on science goals, supplementing this background with post-flash may be a viable solution. For the current example, adding a post-flash of 25e^– on the ETC front page results in the low-background warning no longer triggering, as well as a reduction of the reported S/N because of the increased background. However this extra post-flash would considerably boost the recovered signal for sources far from the serial register, resulting in a net gain in S/N for such sources. The ETC is not currently capable of estimating WFC CTE-induced signal losses. The ACS Team has provided such a calculator, suitable for point-source photometry, at the ACS CTE Calculator website.

The above example should be treated with caution, however, for the following reasons:

• There is nothing particularly ideal about a WFC background of 30 e^–/pixel. In general, a higher background reduces CTE losses at the cost of added noise, and the optimal post-flash level will depend upon source position and intensity.
• The lowest ETC settings for earthshine, airglow, and zodiacal light may occasionally overestimate actual WFC background levels, based upon recent comparisons over the lifetime of ACS (ACS ISR 2022-01). Users especially concerned with CTE should err on the side of lower-than-predicted background when determining how much post-flash to add.
  
• As shown in Figure 9.4, the WFC post-flash illumination declines by 50% with radius from the detector center, with approximately azimuthal symmetry. When the post-flash is the dominant source of background, both the noise properties and the degree of CTE mitigation across the image will therefore be highly nonuniform. The non-uniformity is such that the post-flash signal is highest where CTE losses have the most effect, i.e., far from the amplifier in the parallel transfer direction. As a consequence, mitigation of CTE losses will be best for the sources that need it the most. However, the nonuniform noise of the post-flash background will require a careful treatment during subsequent analyses.
  
• For users desiring to use the post-flash capabilities, it is recommended to read Section 5 of ACS ISR 2018-02. The APT assumes a single value of 14 e^-/sec to compute the flash duration required to achieve a specified signal (e.g., for a 20e^- post-flash, t = 20e^-/(14 e^-/sec) = 1.4 seconds). Due to the nonuniform post-flash signal, this flash rate could be an overestimation of the true post-flash signal at the location of the target. The aforementioned ISR provides a convenient method for computing the necessary scaling factor to ensure the desired number of electrons are deposited at the location of your source.
  

ACS ISR 2018-02 and ACS ISR 2014-01 provide detailed guidance for the appropriate use cases of post-flash.

9.6.7 Example 7: WFC Imaging of a Point Source Taking into Account CTE-related Losses

While the ACS Imaging ETC is an extremely valuable tool to plan observations, it does not take into account how sources are dimmer than expected due to degraded CTE. In this example, we will demonstrate how one can utilize the ETC in combination with the photometric CTE correction formula of ACS ISR 2022-06 to more accurately assess the time needed to detect point sources at fixed signal-to-noise ratio (SNR). This example is presented in more detail in an available Jupyter Notebook.

Our goal is to estimate the exposure time needed to obtain SNR = 10 for a V = 23 mag (Vega system) B5V star using the F658N narrow-band filter. We set up the ETC assuming default backgrounds and the use of the Castelli & Kurucz stellar template. We also use a circular aperture with a radius of 5 pixels (0.25 arcseconds) for our brightness measurement. The ETC tells us we need a total time of 1436 seconds to reach this SNR in a single exposure (# frames = 1), but we need multiple exposures to remove image defects. Let's assume we are doing a two-point line dither, so we set # frames = 2, and get a total time of 1742 seconds, or 2 × 871 seconds. However, the real SNR measured in this exposure time will be less than 10 due to degraded CTE. The specific degree to which sources are dimmed is discussed in ACS ISR 2022-06, which also provides a formula to estimate the true brightness in counts, C_true, as a function of the measured (artificially dimmed by degraded CTE) brightness, C_meas, background, location on the detector, and date. For our purposes, we actually want to invert this formula to estimate C_meas as a function of C_true (and the other parameters), but this is not trivial due to its complex form. One workaround is to generate a curve of C_true vs. C_meas (with all other parameters fixed) and then interpolate to estimate C_meas. The specific Python code to do this task is shown in this Jupyter Notebook. We assume our target is in the middle of one of the WFC detectors (y = 1024 pixels) and our observations take place on MJD = 60766, or April 1, 2026.

The ETC run above tells us that our source should contain a total of 848e^- over both exposures, or C_true = 424e^- per exposure. Using the photometric CTE correction formula, we estimate that this source will actually have a measured brightness of C_meas = 302.5e^- per exposure, corresponding to a magnitude difference of 0.37 mags. In other words, our V = 23 mag star will actually look like a V = 23.37 mag star. Going back to the ETC, we can plug in this magnitude and see that we actually expect SNR = 7.2 in 1742 seconds.

If SNR=7.2 is not satisfactory, users have a few options, the simplest being to move the target closer to the serial registers to minimize the number of pixel transfers during readout. For instance, placing the star 100 pixels from the serial registers yields a measured brightness of C_meas = 411e^- per exposure, only ~12e^- lower than C_true. If this option is not possible, steps should be taken to raise the background and/or source counts per exposure. For compact sources, post-flash may be utilized, but this will have the biggest impact on extremely weak sources. For sources with brightnesses of a few hundred e-, any gains in recovered counts will be typically be outweighed by the added noise from post-flash, lowering the overall SNR (see Figure 5 of ACS ISR 2024-02). Instead, users can increase their exposure time. Keep in mind that once we alter the integration time per exposure, the specific impact of degraded CTE will change because the backgrounds and total source brightnesses per exposure change. Therefore, it may take some iteration to find the optimal exposure time to offset the impact of degraded CTE and reach the desired SNR. 

As a starting point we can use the ETC to see the total exposure time we would need to detect our artificially dimmed V = 23.37 mag star at SNR = 10. It says we need 2759 in two exposures, but we should probably break this into three exposures, so setting # Frames = 3, the ETC says we need 3088 seconds, or 3 × 1029 seconds. Plugging V = 23 and this new exposure time into the ETC gives us the new C_true = 501e- per exposure and an expected background of 21e-, and using photometric CTE correction formula, we expect C_meas = 370e^-, or a magnitude difference of 0.33. Plugging in V = 23.33 into the ETC, we expect SNR = 10.35 with this new exposure time, close to our desired SNR = 10. This new exposure time is a bit higher because the CTE-related losses weren't quite as bad from our three exposure setup as our shorter two exposure setup due to the different exposure times.

This example assumed users would employ the FLT/DRZ images and apply the photometric CTE correction formula to correct the measured brightnesses. Alternatively, users can use the FLC/DRC images which are CTE-corrected according to the pixel-based CTE correction algorithm of ACS ISR 2018-04. However, the photometric accuracy of the pixel-based CTE correction begins to suffer when targets are dimmer than ~500e- per exposure. There tends to be amplified noise in the background of these images as well. The recovered SNR will likely be better than that in images with no CTE correction, however, it will not be perfect.