12.5 High Signal-to-Noise Ratio Observations
The maximum achievable signal-to-noise (S/N) ratio of STIS observations for well exposed targets is, in general, limited by the S/N ratio and stability of the flat fields. CCD flat-field observations are obtained monthly. Ultimately, CCD reference flats in the pipeline should have an effective illumination of up to 106 e–/pix. Thus, it should be possible to achieve a S/N ratio of several hundred over larger spatial scales given sufficient source counts. The limitation is the temporal stability of the CCD reference flats, which show variations of a few tenths of a percent. Dithering techniques can and should be considered for high S/N CCD observations (see Section 11.3). The realizable S/N ratio for spectroscopy will be less in the far red due to fringing, unless appropriate fringe flats are applied (see the caveats on long-wavelength spectroscopy in the red in Section 7.2.4).
Two observing techniques have been employed to obtain higher S/N ratios in STIS CCD spectra of relatively bright stars. In the first method, high total counts are built up by deliberate saturation of the detector at a fixed pointing. The excess charge "bleeds" along the columns, but, for GAIN=4, the total accumulated charge is preserved in each column. In this way, S/N ratios of order 1000 have been achieved (Gilliland et al. 1999, PASP, 111, 1009; Bohlin & Gilliland 2004, AJ, 127, 3508). The second method uses spatial scanning – trailing the target along one of the long STIS slits, roughly perpendicular to the dispersion. The aim is again to build up high total counts in each spectral element, but without saturating the individual pixels in the detector. As discussed in more detail in Section 12.12, spatial scanning can enable better flat fielding, more robust removal of cosmic rays, and more complete removal of the strong fringing seen in STIS CCD spectra at wavelengths longer than about 7000 Å. In a first application of this method, Cordiner et al. (2017, ApJ, 843, L2) achieved S/N ~ 600-800 in G750M spectra near 9300 Å, consistent with expectations based on photon statistics. Two subsequent special calibration programs have demonstrated total flux reproducibility at a level ~30 ppm in repeated G750L spatial scans of the relatively bright exoplanet host star 55 Cnc obtained over several HST orbits (STIS September 2020 STAN).
The S/N ratio of MAMA flat fields is limited by the long integration times needed to acquire them and the limited lamp lifetimes. (See Section 16.1). S/N ratios of ~100:1 should routinely be achievable for spectroscopic observations of bright sources with the MAMAs if supported by counting statistics. If a program requires high S/N ratios, we recommend using some form of dithering (described below) and co-adding the spectrograms to ameliorate the structure in the flat fields.
Kaiser et al. (1998, PASP, 110, 978) and Gilliland (STIS ISR 1998-16) reported quite high S/N ratios for spectrograms of bright standard stars obtained during a STIS commissioning program. The realizable S/N ratio depends on the technique used to correct for the flat-field variations, as shown in Table 12.2. The S/N ratios quoted are for wavelength bins from an extraction box of 2x11 lowres pixels (2 in AXIS1 or dispersion, 11 in AXIS2 or across the dispersion). In the table, the Poisson limit is just the S/N ratio that would be expected on the basis of counting statistics alone; "No Flat" means the realized S/N ratio without applying any flat field to the data; "Reference Flat" means the realized S/N ratio after applying the best available reference flat, and the "Full FP-SPLIT Solution" is discussed under Section 12.5.2 below. Clearly, S/N ratios in excess of 100:1 per resolution element are well within the capabilities of the MAMAs for spectroscopy.
Table 12.2: Results of S/N Ratio Tests with STIS MAMAs in Orbit.
Grating | Poisson Limit | No Flat | Reference Flat | Full FP-Split Solution1 |
| 470 | 200 | 3602 | 390 |
| 295 | 90 | 180 | N/A |
| 400 | 250 | 3203 | 380 |
| 200 | 100 | 150 | N/A |
1 Results obtainable in echelle modes using the FP-SPLIT slits and an iterative solution for the spectrogram and flat field.
2 Results obtained using the FP-SPLIT slits and simply shifting and co-adding the spectrograms after flat fielding.
3 Results obtained using the FP-SPLIT slits and simply shifting and co-adding the spectrograms after flat fielding.
12.5.1 Dithering
In first-order spectroscopic modes, improved S/N ratios can be achieved by stepping the target along the slit, taking separate exposures at each location, which are subsequently shifted and added in post-observation data processing (PATTERN=STIS-ALONG-SLIT, see Section 11.3). This stepping, or dithering, in the spatial direction effectively smooths the detector response over the number of steps, achieving a reduction of pixel-to-pixel nonuniformity by the square root of the number of steps, assuming the pixel-to-pixel deviations are uncorrelated on the scale of the steps. In imaging modes, the same dithering can be done in two dimensions, i.e., the steps need not be along a straight line (see Section 11.3.5). For echelle modes, stepping along the slit is possible only with a long echelle slit (e.g., the 6X0.2 or 52X0.1 apertures, or one of the available but unsupported long-slit apertures), but see Section 12.2 above, and note the ameliorating effects of Doppler smearing as noted below. In practice, using the FP-SPLIT slits (see Section 12.5.2) provides a better means of dithering echelle observations.
In a slitless or wide-slit mode, stepping along the dispersion direction provides another method to achieve high S/N ratio data. Data so obtained permit, at least in principle, an independent solution for spectrogram and flat field, but at a cost of lower spectral resolution and line profile confusion due to the wings of the LSFs transmitted through a wide slit (see Section 13.7). Such an approach for STIS data has not been attempted as of this writing.
The three scanned STIS echelle modes (E140H, E230H, and E230M), have a number of secondary wavelength settings defined with broad overlap in their wavelength coverage. Using two or more of these overlapping wavelength settings is another simple way to move a given feature to different parts of the detector.
12.5.2 FP-SPLIT Slits for Echelle Observations
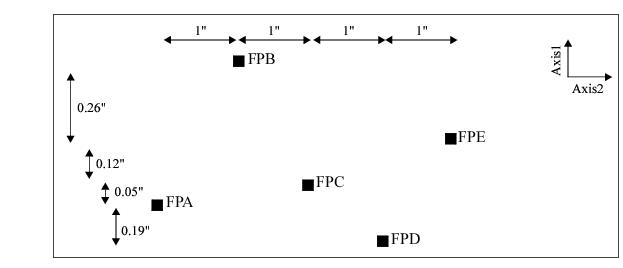
A special kind of dithering in the spectral direction is possible for echelle mode observations with one of two sets of fixed-pattern (or FP-SPLIT) slits. These slit sets are each comprised of a mask with five apertures that are all either 0.2X0.2 or 0.2X0.06 in size. A schematic of the configuration is shown in Figure 12.4. During a visit, the target is moved from one aperture to another, and the slit wheel is repositioned, so that the spectrogram is shifted (relative to the detector pixels) along the dispersion direction only. The slits are spaced to place the spectrogram at different detector locations, so that flat-field variations can be ameliorated by co-adding many such spectrograms. The FP-SPLIT slits can be a good choice for obtaining high S/N ratio echelle data, since it is usually not possible to dither in the spatial direction. However, since S/N=100 is routinely achieved using the normal echelle apertures, the FP-SPLIT slits are rarely used.
AXIS1 corresponds to the dispersion direction, and AXIS2 to the spatial direction. Dimensions are not to scale.The STIS flight software automatically applies an onboard compensation for Doppler motion for echelle and MAMA medium resolution, first-order data taken in ACCUM mode (see Chapter 11). The MAMA control electronics correct (to the nearest highres pixel) the location of each event for the Doppler shift induced by the spacecraft motion prior to updating the counter in the image being collected. Thus, the flat-field correction for any image pixel would be an appropriately weighted average over a small range of nearby pixels, and the effect of spacecraft-induced Doppler shifts is therefore to naturally provide some smoothing over the flat fields in the echelle modes.
Table 12.3: Effect of Doppler Shift on Exposure Times.
Grating | Maximum Doppler Shift (hi-res pixels) | Tmax1 (minutes) |
| 11.41 | 2.7 |
| 4.59 | 7.0 |
| 11.41 | 2.7 |
| 3.00 | 11.3 |
1 For inclination i = 0; actual duration will scale as sec(i). See text for details.
Obtaining the Highest S/N Ratio with the FP-SPLIT Slits
As described above, the FP-SPLIT slits have been used with the echelles to provide signal-to-noise as high as ~350 with the direct shift-and-add method. Additionally, data obtained with the FP-SPLIT slits make it possible to solve independently for the fixed-pattern (i.e., the flat-field variation) and the source spectrum. An iterative technique for combining FP-SPLIT data was applied successfully to data obtained with GHRS (see Lambert et al., ApJ, 420, 756, 1994), based on a method described by Bagnuolo and Gies (ApJ, 376, 266, 1991). This same technique was applied by Gilliland (STIS ISR 1998-16) to STIS observations of a standard star. The S/N ratio that was achieved with these slits is summarized in the last column of Table 12.2, which shows that the FP-SPLIT slits can offer some advantage when one is attempting to achieve the highest possible S/N ratio. In general, though, it may be difficult to improve upon the S/N ratio that can be achieved by simply calibrating with the standard flat field and co-adding the spectrograms.
There are a number of caveats to the use of the FP-SPLIT slits to solve independently for the target spectrum and flat field. The most notable is that the targets must be relatively bright point sources. The restriction to bright targets results both from the need to limit the duration of individual exposures to keep the Doppler-induced spectral shifts to less than one highres pixel, and from the need to have appreciable counts in the individual exposures—at least in the orders of interest. Very high counts in the sum of all exposures are essential for a good (and stable) solution to both the target spectrum and the underlying flat field.
If one is using the FP-SPLIT slits to distinguish the signature of the flat field from the target spectrum, then Doppler smearing (and the discrete compensation for that smearing) will defeat that solution. In this case, the exposures must be kept as short as if there were no Doppler compensation at all if the goal is to solve for the pixel-to-pixel variation at a precision higher than that of the available flat-field reference files.
The utility of FP-SPLIT observations is also limited by the modest range of slit offsets in wavelength space, and by the distribution and character of the features in the target spectrum itself. That is, if the spectrum in the order(s) of interest is dominated by absorption over a width comparable to or larger than the largest offset range, the solution may not be stable or unique. A corollary is that some of the spectral orders must contain moderately prominent spectral features with good signal in order to distinguish the spectrum from flat-field variations. Table 12.4 gives the FP-SPLIT offsets for each grating, including offsets in Ångstroms for typical central-wavelength settings.
Table 12.4: Magnitude of Spectrogram Offset for the FP-SPLIT Slits.
Grating | Minimum Offset | Maximum Offset (hi-res pix) | CENWAVE (Å) | Max. Offset @CENWAVE (Å) |
| 2.128 | 26.383 | 1416 | 0.164 |
| 2.778 | 34.444 | 1425 | 0.535 |
| 2.128 | 26.383 | 2390 | 0.277 |
| 2.857 | 35.429 | 2340 | 1.382 |
-
STIS Instrument Handbook
- • Acknowledgments
- Chapter 1: Introduction
-
Chapter 2: Special Considerations for Cycle 33
- • 2.1 Impacts of Reduced Gyro Mode on Planning Observations
- • 2.2 STIS Performance Changes Pre- and Post-SM4
- • 2.3 New Capabilities for Cycle 33
- • 2.4 Use of Available-but-Unsupported Capabilities
- • 2.5 Choosing Between COS and STIS
- • 2.6 Scheduling Efficiency and Visit Orbit Limits
- • 2.7 MAMA Scheduling Policies
- • 2.8 Prime and Parallel Observing: MAMA Bright-Object Constraints
- • 2.9 STIS Snapshot Program Policies
- Chapter 3: STIS Capabilities, Design, Operations, and Observations
- Chapter 4: Spectroscopy
- Chapter 5: Imaging
- Chapter 6: Exposure Time Calculations
- Chapter 7: Feasibility and Detector Performance
-
Chapter 8: Target Acquisition
- • 8.1 Introduction
- • 8.2 STIS Onboard CCD Target Acquisitions - ACQ
- • 8.3 Onboard Target Acquisition Peakups - ACQ PEAK
- • 8.4 Determining Coordinates in the International Celestial Reference System (ICRS) Reference Frame
- • 8.5 Acquisition Examples
- • 8.6 STIS Post-Observation Target Acquisition Analysis
- Chapter 9: Overheads and Orbit-Time Determination
- Chapter 10: Summary and Checklist
- Chapter 11: Data Taking
-
Chapter 12: Special Uses of STIS
- • 12.1 Slitless First-Order Spectroscopy
- • 12.2 Long-Slit Echelle Spectroscopy
- • 12.3 Time-Resolved Observations
- • 12.4 Observing Too-Bright Objects with STIS
- • 12.5 High Signal-to-Noise Ratio Observations
- • 12.6 Improving the Sampling of the Line Spread Function
- • 12.7 Considerations for Observing Planetary Targets
- • 12.8 Special Considerations for Extended Targets
- • 12.9 Parallel Observing with STIS
- • 12.10 Coronagraphic Spectroscopy
- • 12.11 Coronagraphic Imaging - 50CORON
- • 12.12 Spatial Scans with the STIS CCD
-
Chapter 13: Spectroscopic Reference Material
- • 13.1 Introduction
- • 13.2 Using the Information in this Chapter
-
13.3 Gratings
- • First-Order Grating G750L
- • First-Order Grating G750M
- • First-Order Grating G430L
- • First-Order Grating G430M
- • First-Order Grating G230LB
- • Comparison of G230LB and G230L
- • First-Order Grating G230MB
- • Comparison of G230MB and G230M
- • First-Order Grating G230L
- • First-Order Grating G230M
- • First-Order Grating G140L
- • First-Order Grating G140M
- • Echelle Grating E230M
- • Echelle Grating E230H
- • Echelle Grating E140M
- • Echelle Grating E140H
- • PRISM
- • PRISM Wavelength Relationship
-
13.4 Apertures
- • 52X0.05 Aperture
- • 52X0.05E1 and 52X0.05D1 Pseudo-Apertures
- • 52X0.1 Aperture
- • 52X0.1E1 and 52X0.1D1 Pseudo-Apertures
- • 52X0.2 Aperture
- • 52X0.2E1, 52X0.2E2, and 52X0.2D1 Pseudo-Apertures
- • 52X0.5 Aperture
- • 52X0.5E1, 52X0.5E2, and 52X0.5D1 Pseudo-Apertures
- • 52X2 Aperture
- • 52X2E1, 52X2E2, and 52X2D1 Pseudo-Apertures
- • 52X0.2F1 Aperture
- • 0.2X0.06 Aperture
- • 0.2X0.2 Aperture
- • 0.2X0.09 Aperture
- • 6X0.2 Aperture
- • 0.1X0.03 Aperture
- • FP-SPLIT Slits 0.2X0.06FP(A-E) Apertures
- • FP-SPLIT Slits 0.2X0.2FP(A-E) Apertures
- • 31X0.05ND(A-C) Apertures
- • 0.2X0.05ND Aperture
- • 0.3X0.05ND Aperture
- • F25NDQ Aperture
- 13.5 Spatial Profiles
- 13.6 Line Spread Functions
- • 13.7 Spectral Purity, Order Confusion, and Peculiarities
- • 13.8 MAMA Spectroscopic Bright Object Limits
-
Chapter 14: Imaging Reference Material
- • 14.1 Introduction
- • 14.2 Using the Information in this Chapter
- 14.3 CCD
- 14.4 NUV-MAMA
-
14.5 FUV-MAMA
- • 25MAMA - FUV-MAMA, Clear
- • 25MAMAD1 - FUV-MAMA Pseudo-Aperture
- • F25ND3 - FUV-MAMA
- • F25ND5 - FUV-MAMA
- • F25NDQ - FUV-MAMA
- • F25QTZ - FUV-MAMA, Longpass
- • F25QTZD1 - FUV-MAMA, Longpass Pseudo-Aperture
- • F25SRF2 - FUV-MAMA, Longpass
- • F25SRF2D1 - FUV-MAMA, Longpass Pseudo-Aperture
- • F25LYA - FUV-MAMA, Lyman-alpha
- • 14.6 Image Mode Geometric Distortion
- • 14.7 Spatial Dependence of the STIS PSF
- • 14.8 MAMA Imaging Bright Object Limits
- Chapter 15: Overview of Pipeline Calibration
- Chapter 16: Accuracies
-
Chapter 17: Calibration Status and Plans
- • 17.1 Introduction
- • 17.2 Ground Testing and Calibration
- • 17.3 STIS Installation and Verification (SMOV2)
- • 17.4 Cycle 7 Calibration
- • 17.5 Cycle 8 Calibration
- • 17.6 Cycle 9 Calibration
- • 17.7 Cycle 10 Calibration
- • 17.8 Cycle 11 Calibration
- • 17.9 Cycle 12 Calibration
- • 17.10 SM4 and SMOV4 Calibration
- • 17.11 Cycle 17 Calibration Plan
- • 17.12 Cycle 18 Calibration Plan
- • 17.13 Cycle 19 Calibration Plan
- • 17.14 Cycle 20 Calibration Plan
- • 17.15 Cycle 21 Calibration Plan
- • 17.16 Cycle 22 Calibration Plan
- • 17.17 Cycle 23 Calibration Plan
- • 17.18 Cycle 24 Calibration Plan
- • 17.19 Cycle 25 Calibration Plan
- • 17.20 Cycle 26 Calibration Plan
- • 17.21 Cycle 27 Calibration Plan
- • 17.22 Cycle 28 Calibration Plan
- • 17.23 Cycle 29 Calibration Plan
- • 17.24 Cycle 30 Calibration Plan
- • 17.25 Cycle 31 Calibration Plan
- • 17.26 Cycle 32 Calibration Plan
- Appendix A: Available-But-Unsupported Spectroscopic Capabilities
- • Glossary