13.2 Using the Information in this Chapter

13.2.1 Wavelength Ranges

The complete wavelength range for each grating, as well as the wavelength coverage per tilt for the scanned grating modes, is shown in a table and graphically. The exact wavelengths at the ends of the ranges for the MAMA detectors will depend on the MAMA monthly offsetting. This procedure shifts the spectrogram so that it falls on slightly different parts of the MAMA detectors from month to month in order to minimize charge depletion in the microchannel plates and can cause the loss of ±30 pixels from either end of the spectrogram in dispersion (AXIS1) and ±80 pixels in cross-dispersion (AXIS2). Spectral format plots of the STIS grating and central wavelength settings are available to download from the STIS webpage under "Instrument Design > Gratings/Prism."

Monthly offsetting for the echelles was discontinued in August 2002. Prior to that, the monthly offsetting projected the extreme orders of formats off of the detector in some months.The wavelength ranges for the echelle gratings given in this chapter are those routinely falling on the detector since the discontinuation of the monthly offsets for the echelle modes, as measured from data obtained for the Cycle 17 Calibration Program 11866. The wavelength ranges of archival data taken before August 2002 may differ from those values given here. Users should also be aware that the past monthly offsets have influenced whether or not a given echelle order has a good sensitivity correction; therefore, not all echelle orders available on the detector will be flux calibrated. Users may refer to STIS ISR 2012-01 for more information on the affected orders. Some of these affected orders are expected to be added back to the flux calibrated data products as the flux recalibration effort is completed. See Table 2 of ISR 2024-04 for a list of previously excluded orders.

Wavelengths in this handbook and in STIS data products are always measured in vacuum conditions.

13.2.2 Grating Sensitivities and Throughputs

This chapter contains plots and tables of sensitivities and throughputs for each grating mode. Section 6.2 in the Exposure Time Calculation chapter explains how to use these sensitivities to calculate expected count rates from a source.

The total system¹ spectroscopic point source sensitivity, $//<![CDATA[ \begin{array}{l}S^p_\lambda\end{array} //]]>$, has the unit:
counts/s/pix_λ per incident erg/cm²/s/Å for the MAMA and e^–/s/pix_λ per incident erg/cm²/s/Å for the CCD, where:

• pix_λ = a pixel in the dispersion direction.
• counts refer to the total counts from the point source integrated over the PSF in the direction perpendicular to the dispersion (along the slit).
  
  

The spectroscopic diffuse source sensitivity, $//<![CDATA[ \begin{array}{l}S^d_\lambda\end{array} //]]>$, has the units counts/s/pix_λ/pix_s per incident erg/s/cm²/Å/arcsec² for the MAMA and e^–/s/pix_λ/pix_s per incident erg/s/cm²/Å/arcsec² for the CCD, where:

• pix_λ= a pixel in the dispersion direction.
• pix_s= a pixel in the spatial direction.

$//<![CDATA[ \begin{array}{l}S^p_\lambda\end{array} //]]>$ and $//<![CDATA[ \begin{array}{l}S^d_\lambda\end{array} //]]>$ are related through the relation:

where:

• m_s is the platescale in arcsec per pixel in the direction perpendicular to the dispersion.

• W is the width of the slit used in arcsec.

Here, we have assumed that the diffuse source has a uniform brightness over the area of interest and that the spectrum can be approximated as a continuum source. The throughput is defined as the end-to-end effective area divided by the geometric area of a filled, unobstructed 2.4 meter aperture (see Chapter 6).

Tables of sensitivities and throughputs are given for a point source placed in the center of the largest clear aperture for each detector. Calibration data for measuring sensitivities and throughputs for a point source placed high on the CCD detector in the long-slit "E1" pseudo-apertures (see Section 7.3.8) were taken in Cycles 10 and 11. It was found that the overall low dispersion throughputs are decreased by 2–3%, and the medium dispersion throughputs are expected to show a similar reduction. The sensitivity plots give values for point and diffuse sources. In the plots in this chapter we show the diffuse source sensitivity for a 0.1 arcsec wide slit. For an extended continuum source, $//<![CDATA[ \begin{array}{l}S^d_\lambda\end{array} //]]>$ scales directly with slit width, as above.

For the echelles, the sensitivities given were derived from fits of a smooth curve as a function of wavelength to the measured sensitivities at the central wavelength of each order (i.e., they do not include the effect of the echelle ripple). The Spectroscopic Exposure Time Calculator (ETC; see Chapter 6) will properly take the echelle ripple into account and should be used for more detailed S/N analysis.

Small but significant changes in the STIS sensitivity have been revealed by repeated observations of the same standard stars in the 52X2 slit. These changes are discussed in detail in Section 7.2.4, and Section 7.4.3, and the mean variations in sensitivity with time for some first order configurations are illustrated in Figure 7.1 and in Figure 7.15. Time- and temperature-dependent variations are discussed in STIS ISR 2004-04 and the most recent measurements of these variations can be found in STIS ISR 2017-06. The ETC accounts for the latest sensitivity trends, projected to the mid-point of the current HST Cycle.

13.2.3 Signal-To-Noise Plots

For each grating mode, a plot is provided for estimating the signal-to-noise (S/N) for a class of sources and a range of exposure times, corresponding to a fiducial taken at wavelengths near the peak of the responses. The fiducial wavelength is indicated in the ordinate label of each plot. To estimate signal-to-noise at alternate wavelengths, scale the source flux or magnitude by the relative sensitivities (or throughputs) at the wavelength of interest and at the fiducial. The point source plots show S/N as a function of F_λ and of V+STMAG(λ) for a range of exposure times. The diffuse source plots show I_λ and V+STMAG(λ) per arcsec² for a range of exposure times. Using STMAG units is natural in this plot given that a particular STMAG value corresponds to a flux distribution with a constant value of F_λ. In producing these plots we assumed an average sky background (as described in Chapter 6) and the appropriate values for read noise and dark current for each detector. Note the following:

• The point source S/N has been calculated per two dispersion pixels and has been integrated over the PSF to contain 80% of the flux in the spatial direction.
• The point source S/N calculations assume the use of the 52X0.2 slit for the first-order modes and the use of the 0.2X0.2 slit for the echelle modes.
• The diffuse-source S/N is calculated with the 0.2 arcsecond wide slit and the assumption that the slit is fully filled by a diffuse continuum source. The S/N is given per 2 spatial pixels and 4 spectral pixels for the CCD and is given per 2 spatial pixels and 6 spectral pixels for the MAMA (these are the equivalent spectral resolution elements for these observations).
• For the CCD, the plots assume CR-SPLIT=2 and CCDGAIN=1.
• The different symbols in the S/N figures delineate regions where different sources of noise dominate. A particular source of noise (read noise for example) is presumed to dominate if it contributes more than half the total noise in the observations. Saturation is likewise indicated.
• The vertical dashed line indicates the MAMA bright object observing limits; if F_λ (or I_λ) exceeds the indicated value, the observation would exceed the observing limits (recall that the observing limits are at slightly higher count rates than the screening limits given in Table 13.45). For diffuse sources we indicate only the local rate limit, since the global limit is dependent on the source extent. If no line is seen on the plot, it indicates the limit is higher than the range of fluxes plotted.

These plots are meant to allow a general assessment of the feasibility of proposed scientific program.  In situations requiring more detailed calculations (non-stellar spectra, extended sources, other sky background levels, full treatment of wavelength dependent sensitivity changes, etc.), we refer users to the STIS ETC, available at: http://etc.stsci.edu/ .

Follow these steps to use the S/N plots:

1. Look up in Table 13.1 the spectral type and wavelength region of interest of your target observation (e.g., G0 V @ 4300 Å). Interpolate in the table to get STMAG_λ.
2. Add the V magnitude of the target to the interpolated value of STMAG_λ derived from the table.
3. Find the appropriate plot for the desired grating, and locate V+STMAG_λ on the horizontal axis. Read off the S/N for the desired exposure time, or vice-versa. Alternatively use F_λ directly on the horizontal axis.
4. To get accurate values for repeated or CR-SPLIT exposures, one should use the sub-exposure time when consulting the plot, and then multiply the resulting S/N by $//<![CDATA[ \begin{array}{l}\sqrt{N}\end{array} //]]>$, where N is the number of sub-exposures to be averaged. Recall that these plots assume CR-SPLIT=2 for CCD observations.

We now give a sample S/N calculation using these plots. Consider a V = 18 star of spectral class B0 V, for which we want to derive the S/N for a 100 second CR-SPLIT exposure in G430L with the CCD. We look up the B0 V spectral class and interpolate in the table between 4000 Å (STMAG_λ = –1.20) and 4500 Å (STMAG_λ = –0.78) to obtain STMAG_λ ~–1 at 4300 Å. We thus have V+STMAG_λ = 17. We look at Figure 13.13 and find this value on the horizontal axis. We locate exposure time 100 and find S/N ~ 10. This exposure is well below the saturation lines in the plot, so saturation is not a concern.

13.2.4 Plate Scales

In the grating information section, the plate scale (units: arcsec/pix) is given in the table for each grating. The values used have been obtained from imaging observations and have been approximated at 0.05072 arcsec/pix for the CCD modes, and ~0.0246 and 0.0248 arcsec/pix respectively for the G140L and G230L MAMA modes (see Section 14.6). The other MAMA spectroscopy modes (G140M and G230M) operate at a lower magnification, yielding a cross-dispersion plate scale of ~0.029 arcsec/pix. Anamorphic magnification by the gratings further modifies the plate scales in the dispersion direction, particularly for the echelle modes. The relevant scales in both directions have been used in the generation of each grating's diffuse source sensitivity and signal-to-noise plots.

The exact level of anamorphic magnification is a function of grating and central wavelength. More detailed information on the CCD modes can be found in STIS ISR 1998-23.

13.2.5 Apertures

For each supported slit (aperture) we provide a table giving the name of the slit, length (in the spatial direction) and width (in the dispersion direction) of the slit as well as a table and plot of the relative throughput of the slit (with respect to a large clear aperture) as a function of wavelength. Recall that the point source sensitivities that we have derived assume zero slit losses. Calculations of exposure times must account for light losses for the desired slit. Aperture throughputs measured in orbit are given in STIS ISR 1998-20 and STIS ISR 1998-25. These measurements were used to revise pre-launch models of the aperture throughputs as a function of wavelength, and these revised models were then used to calculate the aperture throughput information given in this chapter and in the aperture throughputs (APERTAB) reference file. Low order flat (LFLTFILE) reference files are used to correct the system throughput as a function of position on the detector, as indicated in the descriptions of the E1, E2, and D1 pseudo-apertures. Since September 2005, additional wavelength-dependent corrections to the throughput have been made for grating-aperture combinations (gac) using the GACTAB reference file. (See Section 3.4.13 in the STIS Data Handbook.) This file currently has entries for the CCD L gratings and long-slit apertures, including the E1 apertures.

13.2.6 Fiducials on Bars

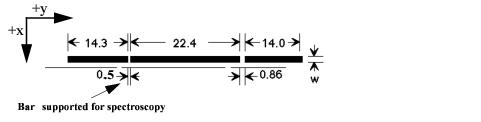
Each STIS long slit has two fiducial bars, located 11.2 arcseconds above and below the slit center, that are 0.86 and 0.5 arcseconds long, respectively (see Figure 13.1 below). They have several purposes. First, the bars provide structural integrity for the long slits. Second, the image of the bars obtained in wavecal (and target acquisition) images is used by the calibration software to locate the projection of the aperture on the detector in post-observation data processing. Lastly, the bars can be used to occult a source thereby providing a coronagraphic spectroscopic capability for STIS. Use of the 0.5 arcsecond bar is supported only on the 52X0.2 slit (the 52X0.2F1 aperture) for coronagraphic observations. Section 12.10 provides more information about performing coronagraphic spectroscopy, and Section 13.7.3 lists some caveats.  As a reminder, for first-order MAMA modes, the projection of the aperture centers onto the detectors varies with the monthly offsetting, and the FUV modes are offset from the detector center by ~3'' (see Section 7.6 for more details).

13.2.7 Spatial Profiles

For each grating mode, information about the cross dispersion (spatial) profiles is provided as follows:

• Plots of model fits to on-orbit data of the spectral profile in the cross dispersion (spatial) direction for a series of central wavelengths and gratings.
• A table of "encircled energies" containing two values: the percent of the total flux contained in the default calibration pipeline 1-D spectrum extraction aperture and the percent of the total flux contained in the central pixel.

13.2.8 Line Spread Functions (Instrumental Profiles)

We show plots of predicted line spread functions (LSFs) for CCD and MAMA spectroscopic modes (Section 13.6), as a function of wavelength and slit width. These plots are based on models of the PSFs at the aperture plane and detector PSFs that have been updated and verified using on-orbit data.  Tabulations of the line spread functions may be found on the STIS Spectral Resolution web page.

Table 13.1: STMAG_λ as a Function of Wavelength for Stellar Objects.

STMAG_λ is defined as the color-dependent correction from V magnitude to STMAG at wavelength λ. The results presented in this table are for Kurucz (1993), solar abundance main-sequence models. The spectral energy distributions of real stars can differ substantially, especially in the ultraviolet (UV), due to differences in chemical composition, surface gravity, and reddening. Also note that these models only include the photospheric continuum and not the chromospheric emission that dominates the flux of most cool stars in the FUV.

Table 13.2: STMAG_λ as a Function of Wavelength for Non-Stellar Objects. 

STMAG_λ is defined as the color-dependent correction from V magnitude to STMAG at wavelength λ.

How to Use the STMAG_λ Tables

1. Interpolate in the table to get STMAG_λ for the spectral type and wavelength region of your target observation (e.g., 6000K star @ 4300 Å).
2. Add the target V magnitude to the STMAG_λ derived from Step 1.
3. Find the S/N plot for the grating you want to use.
4. Locate V+STMAG_λ on the horizontal axis and read off the S/N for the desired exposure time (or read off the exposure time for the desired S/N).

¹ STIS plus HST Optical Telescope Assembly (OTA).