6.5 Detector and Sky Backgrounds
When calculating expected signal-to-noise ratios or exposure times, the background from the sky and the background from the detector must be taken into account.
6.5.1 Detector Backgrounds
Table 6.1 shows the read noise and dark current characteristics of the detectors, taken from Chapter 7. Note that the FUV MAMA detector background is highly variable and this should be taken into account when observing faint sources. See the discussion in sections 4.2.3 and 7.5.2 for additional details.
Table 6.1: Detector Backgrounds.
Background | CCD |
|
|
|---|---|---|---|
Read noise | 6.5 (for | 0 | 0 |
Dark current | ~3.3 × 10–2 e–/s/pix | ~1.1 × 10–3 counts/s/pix | (0.07–6.0) × 10–4, 2 counts/s/pix |
1 To convert to counts/s/pix for CCDGAIN=4, divide by 4.016.
2 Varies widely with position on detector and time since high-voltage turn-on.
6.5.2 Sky Background
The sources of sky background which will affect STIS observations include:
- Earthshine (ES)
- Zodiacal light (ZL)
- Geocoronal emission (GC)
The continuum background in counts/s/pix for spectroscopic observations can be computed as:
| B^{\lambda}_{sky}=\frac{I_\lambda \times S^d_\lambda}{G}~, |
where:
- Iλ is the surface brightness of the sky background, in ergs/s/cm2/Å/arcsec2;
- S^d_\lambda is the diffuse-source sensitivity for the grating mode.
The background in counts/s/pix for imaging observations can be computed as:
| B^{\lambda}_{sky}=\frac{\int I_\lambda \times S^d_\lambda d_\lambda}{G}~, |
where:
- Iλ is the surface brightness of the sky background, in ergs/s/cm2/Å/arcsec2;
- S^d_\lambda is the diffuse-source sensitivity for the imaging mode.
- The integral is over the bandpass.
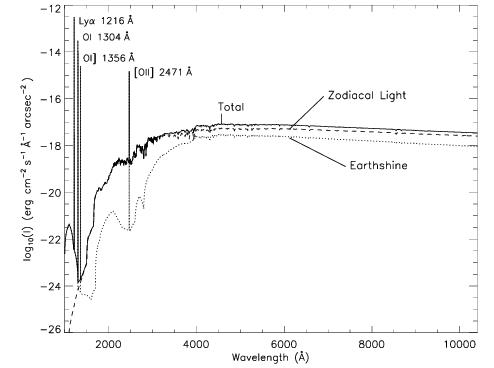
In Figure 6.1 we plot the "high" zodiacal light and earthshine background intensity as a function of wavelength, identifying the separate components which contribute to the background. The information in this figure is presented in tabular form in Table 6.4. In the ETCs and in this Handbook, the choices for earthshine of "shadow," "average," and "extremely high" correspond to 0%, 50% of, and twice the "high" values in Table 6.4. For the zodiacal sky background, the values in Table 6.4 correspond to a high value of mV = 22.1 arcsec–2 from Table 6.2, while the low and average zodiacal light are scaled to mV = 23.3 arcsec–2 and 22.7 arcsec–2, respectively. The strength of the geocoronal (airglow) line emissions are as shown in Table 6.5; the “average” values of these are plotted in Figure 6.1.
Background Variations and LOW-SKY
In the UV the background contains important contributions from airglow lines. These vary from day to night and as a function of HST orbital position. The airglow lines are an important consideration for imaging mode observations and can be for spectroscopic observations as well. Away from the airglow lines, at wavelengths shortward of ~3000 Å, the background is dominated by zodiacal light and is generally much lower than the intrinsic detector background. The contribution of zodiacal light does not vary dramatically with time and varies by only a factor of about three throughout most of the sky. Table 6.2 gives the variation of the zodiacal background as a function of helio ecliptic latitude and longitude. For a target near ecliptic coordinates of (50,0) or (–50,0), the zodiacal light is relatively bright at mv = 20.9 arcsec–2, i.e., about 9 times the polar value of mv = 23.3 arcsec–2.
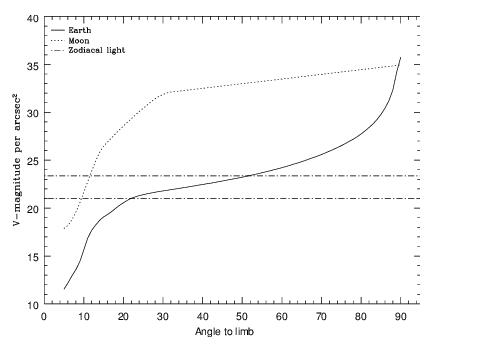
Earthshine, on the other hand, varies strongly depending on the angle between the target and the bright Earth limb. The variation of the earthshine as a function of limb angle from the sunlit Earth is shown in Figure 6.2. The figure also shows the contribution of the Moon which is typically much smaller, and the full range of the zodiacal contribution. For reference, the limb angle is approximately 24° when the HST is aligned toward its orbit pole (i.e., the center of the CVZ).
Table 6.2: Approximate Zodiacal Sky Background in V magnitude arcsec–2 as a Function of Helioecliptic Coordinates, sourced from
Helioecliptic | Helioecliptic Latitude (deg) | ||||||
0° | 15° | 30° | 45° | 60° | 75° | 90° | |
180° | 22.0 | 22.3 | 22.6 | 22.9 | 23.1 | 23.3 | 23.2 |
165° | 22.2 | 22.4 | 22.7 | 22.9 | 23.2 | 23.3 | 23.2 |
150° | 22.3 | 22.5 | 22.8 | 23.0 | 23.2 | 23.3 | 23.2 |
135° | 22.4 | 22.5 | 22.8 | 23.1 | 23.2 | 23.3 | 23.2 |
120° | 22.3 | 22.5 | 22.8 | 23.1 | 23.2 | 23.3 | 23.2 |
105° | 22.1 | 22.4 | 22.8 | 23.0 | 23.2 | 23.2 | 23.2 |
90° | 21.9 | 22.2 | 22.6 | 22.9 | 23.1 | 23.2 | 23.2 |
75° | 21.6 | 22.1 | 22.5 | 22.8 | 23.0 | 23.2 | 23.2 |
60° | 21.2 | 21.8 | 22.3 | 22.6 | 23.0 | 23.1 | 23.2 |
45° | SA | 21.3 | 22.0 | 22.4 | 22.8 | 23.1 | 23.2 |
30° | SA | SA | SA | 22.2 | 22.7 | 23.0 | 23.2 |
15° | SA | SA | SA | SA | 22.5 | 23.0 | 23.2 |
0° | SA | SA | SA | SA | 22.5 | 23.0 | 23.2 |
Note: A value of “SA” denotes positions in the solar avoidance zone.
Table 6.3 contains the expected count rates from different sky backgrounds in various STIS modes, which you can use to determine whether your observations would be background limited.
Observations of the faintest objects may need the special requirement LOW-SKY in the Phase II observing program. LOW-SKY observations are scheduled during the part of the year when the zodiacal background is no more than 30% greater than the minimum possible value for the given sky position. LOW-SKY also invokes the restriction that exposures will be obtained at angles greater than 40° from the bright Earth limb to minimize earthshine and the UV airglow lines. The LOW-SKY special requirement limits the times at which targets within 60° of the ecliptic plane will schedule and limits visibility to about 48 minutes per orbit.
The ETC provides the user with the flexibility to separately adjust both the zodiacal (none, low, average, high) and earthshine (none, average, high, extremely high) sky background components in order to determine if LOW-SKY is advisable for a given program. However, the absolute sky levels that can be specified in the ETC may not be achievable for a given target. As shown in Table 6.2, the minimum zodiacal background level for an ecliptic target is mv = 22.4, which is brighter than both the low and average options with the ETC. By contrast, a target near the ecliptic pole would always have a zodiacal=low background in the ETC. The user is cautioned to carefully consider sky levels as the backgrounds obtained in HST observations can cover significant ranges.
Table 6.3: Count Rates by Sky Background and STIS Mode.
Mode | Count Rates (counts/s/pix) | ||||
Zodiacal1 | Earthshine + Geocoronal Lines | ||||
Ex. High Earth2 | High Earth3 | Avg. Earth4 | Shadow Earth5 | ||
CCD Clear | 1.0 × 10–1 | 9.1 × 10–2 | 4.6 × 10–2 | 2.3 × 10–2 | 3.9 × 10–6 |
CCD Longpass | 6.1 × 10–2 | 5.1 × 10–2 | 2.6 × 10–2 | 1.3 × 10–2 | 1.7 × 10–10 |
| 6.2 × 10–5 | 4.5 × 10–3 | 4.5 × 10–3 | 2.3 × 10–3 | 3.6 × 10–4 |
| 5.7 × 10–5 | 7.1 × 10–4 | 7.0 × 10–4 | 3.5 × 10–4 | 4.5 × 10–6 |
| 5.5 × 10–5 | 2.5 × 10–4 | 2.5 × 10–4 | 1.3 × 10–4 | 1.2 × 10–6 |
| 2.1 × 10–8 | 4.3 × 10–2 | 4.3 × 10–2 | 2.1 × 10–2 | 3.9 × 10–3 |
| 1.9 × 10–8 | 2.6 × 10–3 | 2.5 × 10–3 | 1.3 × 10–3 | 2.0 × 10–5 |
| 1.8 × 10–8 | 1.5 × 10–8 | 1.4 × 10–8 | 6.8 × 10–9 | 6.3 × 10–11 |
| 1.4 × 10–11 | 3.2 × 10–3 | 3.2 × 10–3 | 1.6 × 10–3 | 3.1 × 10–4 |
1 Zodiacal contribution is the same as in Figure 6.1 and Table 6.4 (mV=22.1 arcsec–2).
2 Corresponds to HST pointing 24° from the limb of the sunlit Earth.
3 Corresponds to HST pointing around 38° from the limb of the sunlit Earth, where the earthshine is 50% of the "extremely high" value.
4 Corresponds to HST pointing around 50° from the limb of the sunlit Earth, where the earthshine is 25% of the "extremely high" value.
5 Earthshine for shadow is 0 in the continuum, while the UV geocoronal emission lines are reduced from the high to the low values in Table 6.5.
Geocoronal Emission and Shadow
Background due to geocoronal emission originates mainly from hydrogen and oxygen atoms in the exosphere of the Earth. The emission is concentrated in a very few lines. The brightest line is Lyman-α at 1216 Å. The strength of the Lyman-α line varies between about 2 and 20 kilo-Rayleighs (i.e., between 6.1 × 10–14 and 6.0 × 10–13 ergs/s/cm2/arcsec2 where 1 Rayleigh = 106 photons/s/cm2/[4π steradians]) depending on the time of the observation and the position of the target relative to the Sun. The next strongest contribution is from the triplet O I 1302, 1304, 1306 Å, which rarely exceeds 10% of Lyman-α. The typical strength of the O I 1302 Å triplet is about 2 kilo-Rayleighs (which corresponds to about 5.7 × 10–14 ergs/s/cm2/s/arcsec2) at the daylight side and about 150 times fainter on the night side of the HST orbit. O I] 1356 Å and [O II] 2471 Å lines may appear in observations on the daylight side of the orbit, but these lines are at least 10 times weaker than the O I 1302 Å lines. The widths of the lines also vary. The line widths given in Table 6.5 are representative values assuming a temperature of 2000 K.
The geocoronal emission lines are unresolved at the first-order resolutions of STIS but the emission fills the slit in the spatial dimension. A wider slit or slitless observing does not increase the background counts per pixel from geocoronal emission but does increase the area (range of wavelengths or pixels in the dispersion direction) over which that background is received. Observations with a slit which is n pixels wide in dispersion will be affected by geocoronal emission in a roughly n pixel region centered on the relevant geocoronal emission line wavelength. For slitless spectroscopy in the UV, the effects of geocoronal emission must be taken into account at all pixels, unless a longpass filter is employed to block off the short wavelength emission (see also Section 5.3.5 and Section 12.1).
It is possible to request that exposures be taken when HST is in the umbral shadow of the earth to minimize geocoronal emission (e.g., if you are observing weak lines at ~1216 or ~1304 Å) using the special requirement SHADOW. Exposures using this special requirement are limited to roughly 25 minutes per orbit, exclusive of the guide-star acquisition (or reacquisition) and can be scheduled only during a small percentage of the year. SHADOW reduces the contribution from the geocoronal emission lines by roughly a factor of ten, while the continuum earthshine is set to 0. If you require SHADOW, you should request it in your Phase I proposal (see the Call for Proposals).
An alternate strategy for reducing the effects of geocoronal emissions is to use time resolved observations, so that any data badly affected by geocoronal emission can simply be excluded from the final co-addition. This can be done either by doing the observations in TIME-TAG mode or by just taking a series of short (~5 min) ACCUM mode exposures over the course of each orbit.
Observers should also remember that geocoronal lines will also produce weak absorption features in the spectra of extended targets.
-
STIS Instrument Handbook
- • Acknowledgments
- Chapter 1: Introduction
-
Chapter 2: Special Considerations for Cycle 33
- • 2.1 Impacts of Reduced Gyro Mode on Planning Observations
- • 2.2 STIS Performance Changes Pre- and Post-SM4
- • 2.3 New Capabilities for Cycle 33
- • 2.4 Use of Available-but-Unsupported Capabilities
- • 2.5 Choosing Between COS and STIS
- • 2.6 Scheduling Efficiency and Visit Orbit Limits
- • 2.7 MAMA Scheduling Policies
- • 2.8 Prime and Parallel Observing: MAMA Bright-Object Constraints
- • 2.9 STIS Snapshot Program Policies
- Chapter 3: STIS Capabilities, Design, Operations, and Observations
- Chapter 4: Spectroscopy
- Chapter 5: Imaging
- Chapter 6: Exposure Time Calculations
- Chapter 7: Feasibility and Detector Performance
-
Chapter 8: Target Acquisition
- • 8.1 Introduction
- • 8.2 STIS Onboard CCD Target Acquisitions - ACQ
- • 8.3 Onboard Target Acquisition Peakups - ACQ PEAK
- • 8.4 Determining Coordinates in the International Celestial Reference System (ICRS) Reference Frame
- • 8.5 Acquisition Examples
- • 8.6 STIS Post-Observation Target Acquisition Analysis
- Chapter 9: Overheads and Orbit-Time Determination
- Chapter 10: Summary and Checklist
- Chapter 11: Data Taking
-
Chapter 12: Special Uses of STIS
- • 12.1 Slitless First-Order Spectroscopy
- • 12.2 Long-Slit Echelle Spectroscopy
- • 12.3 Time-Resolved Observations
- • 12.4 Observing Too-Bright Objects with STIS
- • 12.5 High Signal-to-Noise Ratio Observations
- • 12.6 Improving the Sampling of the Line Spread Function
- • 12.7 Considerations for Observing Planetary Targets
- • 12.8 Special Considerations for Extended Targets
- • 12.9 Parallel Observing with STIS
- • 12.10 Coronagraphic Spectroscopy
- • 12.11 Coronagraphic Imaging - 50CORON
- • 12.12 Spatial Scans with the STIS CCD
-
Chapter 13: Spectroscopic Reference Material
- • 13.1 Introduction
- • 13.2 Using the Information in this Chapter
-
13.3 Gratings
- • First-Order Grating G750L
- • First-Order Grating G750M
- • First-Order Grating G430L
- • First-Order Grating G430M
- • First-Order Grating G230LB
- • Comparison of G230LB and G230L
- • First-Order Grating G230MB
- • Comparison of G230MB and G230M
- • First-Order Grating G230L
- • First-Order Grating G230M
- • First-Order Grating G140L
- • First-Order Grating G140M
- • Echelle Grating E230M
- • Echelle Grating E230H
- • Echelle Grating E140M
- • Echelle Grating E140H
- • PRISM
- • PRISM Wavelength Relationship
-
13.4 Apertures
- • 52X0.05 Aperture
- • 52X0.05E1 and 52X0.05D1 Pseudo-Apertures
- • 52X0.1 Aperture
- • 52X0.1E1 and 52X0.1D1 Pseudo-Apertures
- • 52X0.2 Aperture
- • 52X0.2E1, 52X0.2E2, and 52X0.2D1 Pseudo-Apertures
- • 52X0.5 Aperture
- • 52X0.5E1, 52X0.5E2, and 52X0.5D1 Pseudo-Apertures
- • 52X2 Aperture
- • 52X2E1, 52X2E2, and 52X2D1 Pseudo-Apertures
- • 52X0.2F1 Aperture
- • 0.2X0.06 Aperture
- • 0.2X0.2 Aperture
- • 0.2X0.09 Aperture
- • 6X0.2 Aperture
- • 0.1X0.03 Aperture
- • FP-SPLIT Slits 0.2X0.06FP(A-E) Apertures
- • FP-SPLIT Slits 0.2X0.2FP(A-E) Apertures
- • 31X0.05ND(A-C) Apertures
- • 0.2X0.05ND Aperture
- • 0.3X0.05ND Aperture
- • F25NDQ Aperture
- 13.5 Spatial Profiles
- 13.6 Line Spread Functions
- • 13.7 Spectral Purity, Order Confusion, and Peculiarities
- • 13.8 MAMA Spectroscopic Bright Object Limits
-
Chapter 14: Imaging Reference Material
- • 14.1 Introduction
- • 14.2 Using the Information in this Chapter
- 14.3 CCD
- 14.4 NUV-MAMA
-
14.5 FUV-MAMA
- • 25MAMA - FUV-MAMA, Clear
- • 25MAMAD1 - FUV-MAMA Pseudo-Aperture
- • F25ND3 - FUV-MAMA
- • F25ND5 - FUV-MAMA
- • F25NDQ - FUV-MAMA
- • F25QTZ - FUV-MAMA, Longpass
- • F25QTZD1 - FUV-MAMA, Longpass Pseudo-Aperture
- • F25SRF2 - FUV-MAMA, Longpass
- • F25SRF2D1 - FUV-MAMA, Longpass Pseudo-Aperture
- • F25LYA - FUV-MAMA, Lyman-alpha
- • 14.6 Image Mode Geometric Distortion
- • 14.7 Spatial Dependence of the STIS PSF
- • 14.8 MAMA Imaging Bright Object Limits
- Chapter 15: Overview of Pipeline Calibration
- Chapter 16: Accuracies
-
Chapter 17: Calibration Status and Plans
- • 17.1 Introduction
- • 17.2 Ground Testing and Calibration
- • 17.3 STIS Installation and Verification (SMOV2)
- • 17.4 Cycle 7 Calibration
- • 17.5 Cycle 8 Calibration
- • 17.6 Cycle 9 Calibration
- • 17.7 Cycle 10 Calibration
- • 17.8 Cycle 11 Calibration
- • 17.9 Cycle 12 Calibration
- • 17.10 SM4 and SMOV4 Calibration
- • 17.11 Cycle 17 Calibration Plan
- • 17.12 Cycle 18 Calibration Plan
- • 17.13 Cycle 19 Calibration Plan
- • 17.14 Cycle 20 Calibration Plan
- • 17.15 Cycle 21 Calibration Plan
- • 17.16 Cycle 22 Calibration Plan
- • 17.17 Cycle 23 Calibration Plan
- • 17.18 Cycle 24 Calibration Plan
- • 17.19 Cycle 25 Calibration Plan
- • 17.20 Cycle 26 Calibration Plan
- • 17.21 Cycle 27 Calibration Plan
- • 17.22 Cycle 28 Calibration Plan
- • 17.23 Cycle 29 Calibration Plan
- • 17.24 Cycle 30 Calibration Plan
- • 17.25 Cycle 31 Calibration Plan
- • 17.26 Cycle 32 Calibration Plan
- Appendix A: Available-But-Unsupported Spectroscopic Capabilities
- • Glossary